ხელმისაწვდომი უსასრულობის ფილოსოფია, ანუ მათემატიკური განუზღვრელობა

რედაქტორი: გელა გელაშვილი

კორექტორი: მარიამ გორდაძე

მდევარი, 2025

წინათქმა

მითოლოგიით დავიწყოთ. ერთხელ ახალგაზრდა პიროვნებამ საკუთარ თავს ჰკითხა, – როდესაც დამზერად სამყაროში ყველაფერს აქვს დასაწყისი და დასასრული, როცა სხვაგვარს ვერაფერს ხედავ, როგორ უნდა გაჩენილიყო აზრი უთავბოლო, შემოუსაზღვრელი სიდიდის შესახებ? ახალგაზრდა პიროვნებამ დაიწყო ფიქრი პირველ ადამიანებზე, რომლებიც, ალბათ, გარემოებაში მხოლოდ კანონზომიერებებს ამჩნევდნენ, ერთმანეთში გარდამავალ წესრიგს. ამიტომაც, თუკი დაინტერესებოდნენ, რა იყო მანამდე, ვიდრე თვითონ, ვიდრე არსებობა, ლოგიკურად ჩათვლიდნენ, რომ იქნებოდა ის, რაც ახლა არ არის, ანუ შებრუნებული – უწესრიგობა (და ასეცაა უძველესი ცივილიზაციის მითებშიც). თუკი არსებობისას ყველაფერი იწყება და მთავრდება, არსებობამდელ ქაოსში უნდა ყოფილიყო დაუსრულებლობა. ახალგაზრდა პიროვნება მოსაზრებულმა პასუხმა დააკმაყოფილა და ფიქრიანი ცხოვრება განაგრძო.

ამ სტატიაში მითოლოგია ამით ამოიწურა. თუმცა კარგი მაგალითი გვაქვს უსასრულობის იდეასთან დაკავშირებული იმ მეტაფიზიკური ჭმუნვებისა, რითაც უკანასკნელი სამასი ათასწლეულია ერთმანეთს გული შევუღონეთ. ჩვენი ისტორია ასეთია, როდესაც შფოთიანი აზრების იქით, ხელჩასაჭიდი ბევრი არაფერი მოგვეპოვება, ვმსჯელობთ განურჩეველი მიმართულებით. შემდეგ, ვიღაც სხვა, მომავალი ადამიანი ჩვენი ნააზრევის რომელიმე მიმართულებას შედარებით სარწმუნოდ მიიჩნევს, თავის მრავალმიმართულებიან ფიქრს დაუსაფუძვლებს და სადღაც, იმედის იდეალი გახალისდება, ემანდ მოხერხდეს და კაცობრიობა ჭეშმარიტებას დაუახლოვდესო. მოკლედ, შემოუსაზღვრელის, ანუ უსასრულობაზე ფიქრის გზა იყო ეკლიანი, რომელიც (მომავალ გვერდებში აღწერილი გარემოებების გამო) მიუწვდომლობის, ბუნდოვანების, ხშირად ზაფრის და უარესი, მისტიკურობის საბურველში გაეხვა.

მოცემულ სტატიაში შევეცდები უსასრულობა წარმოვაჩინო არა როგორც გაუთავისებელი, დაუმზერელი, შეუცნობელი სიდიდე, არამედ ხელშესახები, კანონზომიერი და ცხადი სამყაროს აღმწერი არაჩვეულებრივი საშუალება. ამისათვის მსჯელობა დაეფუძნება მათემატიკურ დარგებს, – კალკულუსს, კომპლექსური ცვლადის ანალიზსა და სიმრავლეთა თეორიას. მინდა, ცხადად აღვნიშნო, რომ სტატიის არსებითი მიზანი მსჯელობის საყოველთაოობაა,- ფილოსოფიურ და მათემატიკურ ნაწილებს განვიხილავ ისე, რომ უმარტივესად აღქმადი იყოს ნებისმიერი დისციპლინის სპეციალისტისათვის, ტექნიკური ან ჰუმანიტარული ცოდნის წინაპირობის განურჩევლად.

უპირველესად, ვისაუბრებ სააზროვნო საქმეში ყველაზე არსებითის, ფიქრის ფარდობითობის შესახებ. აღწერილს მოჰყვება სტატიის არსებითი ნაწილი, მარტივი მათემატიკური საზრისებით უსასრულობის ხელმისაწვდომი ბუნების ახსნა რიმანის სფეროს, მათემატიკური ზღვრის, უსასრულო კრებადი ჯამებისა და სიმრავლეთა თეორიის მიხედვით.

ფიქრის ფარდობითობა

“არ დავკარგულვარ, რადგანაც ვიცი სადაც ვარ.
თუმცაღა ის, სადაც ვარ, შეიძლება ნიშნავს, რომ დავიკარგე”
–ვინი პუჰი, ა.ა. მილნი

ზოგადად, ისევე, როგორც ყველა ფიზიკის გაკვეთილი მეშვიდე კლასში, ნებისმიერი სააზროვნო საქმიანობა ფარდობითობის გაშინაგნებით უნდა დავიწყოთ. ფარდობითობაში ვგულისხმობ, რომ ადამიანისაგან შეფასებადი ყველა სიმართლე, ყველა მდგომარეობა რაღაცის მიმართ გაიაზრება. სიმარტივისთვის, თქმული ავხსნათ ზუსტად ისე, როგორადაც ზემოხსენებულ ფიზიკის გაკვეთილზე მოხდებოდა და წუთით დავფიქრდეთ მოძრაობაზე. იმისათვის, რომ აღვიქვათ გადაადგილება, საჭიროა, ჩვენი მდებარეობა შევაფასოთ გარემოზე დაკვირვებით,- მაგალითად, თუ მე აღარ ვდგავარ იმ ხესთან, რომელთანაც ვიდექი, ნიშნავს, რომ მას მოვშორდი, გადავადგილდი, მოძრაობა შედგა. თუკი ჩემ გარშემო დამზერადი არაფერია, თუნდაც ასფალტი ფეხებქვეშ, მე ვერასოდეს აღვიქვამ, რომ ვიმოძრავე. ზემოხსენებული ფიზიკის გაკვეთილზე ამ ხეს “ათვლის სხეულს” უწოდებდნენ და იტყოდნენ, რომ მოძრაობა ფარდობითია. ყველა აღქმას, გააზრებას, დიალექტიკურ მსჯელობასა თუ გაზომვას, ესაჭიროება დასაფუძვლებული მოცემულობა, რაღაც განსაზღვრული და უეჭველობად მიჩნეული, რაც იქნება ორიენტირი, ზოგადად რომ შევძლოთ ფიქრი, შეფასება. საგულისხმო აქ ისაა, რომ “ათვლის სხეულის” ცვლილებასთან ერთად, აღქმის თანმიმდევრულობა იცვლება. ვგულისხმობ, გადამწყვეტია იმის მნიშვნელობა, რასაც წინაპირობად მივიღებთ ხოლმე. საბუნებისმეტყველო მეცნიერებებში ხშირია შემთხვევა, როცა აღმოჩნდება, რომ შედეგამდე ვერ მიდიხარ, რადგან ეტალონად შერჩეული წინაპირობა ცუდადაა განსაზღვრული, მასზე დაფუძნებულ მოქმედებებს იმ გზით მიჰყავხარ, შედეგამდე რთულად (ან საერთოდაც ვერ) მიგიყვანს.

მომავალ თავებში ჩვენ ხშირად ვახსენებთ ფარდობითობას, საკითხზე მსჯელობისას მრავალჯერ აღვნიშნავთ, რომ დასკვნამდე ფიქრს წინაპირობა უნდა გამოვუცვალოთ, ანუ სხვა მხრიდან უნდა მივუდგეთ. მოცემულ სტატიაში უსასრულობის შესახებ მეტაფიზიკური აზრის, ცნების ბუნდოვანებისა და ხელმიუწვდომლობის კრიტიკა სწორედ ამ თავში განხილულ საკითხს დაეფუძნება.

თითის წვერი უსასრულობაში

ახლა, სიცხადისათვის, უმშვენიერესი მათემატიკური მოდელის ასახსნელად იდიოტურ ალეგორიას გამოვიყენებ. მკითხველმა წარმოიდგინოს შუაზე გადაჭრილი, საოცრად მრგვალი ფორთოხალი, რომელიც ჭრილის მხრიდან კიდევ უფრო გასაოცრად ბრტყელ მაგიდაზე დევს. რადგანაც ველურად ვფანტაზიორობთ, დავამატოთ კიდევ ერთი პირობა,- მაგიდის ზედაპირიდან ნებისმიერი მიმართულებით წრფივად ნემსების გასროლაა შესაძლებელი. ვთქვათ, რომ რატომღაც გვინდა, გადაჭრილი ფორთოხლის უკიდურესად ზედა წერტილს, ფორთოხლის პოლუსს, მაგიდიდან ნასროლი ნემსი მოვარტყათ. საინტერესო აქ ისაა, რომ საიდანაც არ უნდა გავისროლოთ, სამიზნეს ვერასოდეს მივწვდებით. რაც უფრო შორი წერტილიდან ვესვრით ფორთოხალს, ნემსი პოლუსს უფრო და უფრო დაუახლოვდება, მაგრამ ზუსტად მას ვერაფრით მოხვდება, სულ რომ სამყაროს ყველაზე დიდი მაგიდა გვქონდეს; გეომეტრია ასე მუშაობს. ესაა მდგომარეობა, როდესაც ფორთოხლის უკიდურესად ზედა წერტილი მაგიდიდან უსასრულობაშია.

მიუხედავად იმისა, რომ ახლა ცხადი განუზღვრელობა აღვწერეთ, ალეგორიაზე არანაკლებ იდიოტური სიმარტივით, ჩვენ, დამკვირვებლებს, შეგვიძლია უბრალოდ ავწიოთ საჩვენებელი თითი და ფორთოხლის პოლუსს დავადოთ. ეს ყველაფერი ასე იმიტომ ხდება, თითის წვერზე უსასრულობა იმიტომ გვეტევა, რომ სამგანზომილებიანი არსებები ვართ და მაგიდის სიბრტყიდან, ანუ ორგანზომილებიანი მოდელიდან მიუწვდომელი, ჩვენთვის ხელის გაწვდენამდე ახლოა; ესაა მდგომარეობა, როცა უსასრულობა ცხადია, განსაზღვრულია, ხელშესახებია. ჩვენ ამას ავხსნით.

ახლა პირველად ვახსენებთ სტატიის დასაწყისში განხილულ ფიქრის ფარდობითობას. ფორთოხლის პოლუსის მდებარეობის შეფასებამდე წინაპირობად არჩეული ათვლის სხეულია ის, რაც ამ წერტილს ჯერ უსასრულობად და შემდეგ განსაზღვრულობად აქცევს. თუ ჩვენ ვემყარებით ორგანზომილებიან სიბრტყეს (მაგიდას), მის მიმართ ვმსჯელობთ, ჩვენი “ათვლის სხეულია”, მაშინ ფორთოხლის პოლუსი ხელმიუწვდომელ, შეუცნობელ, ავ უსასრულობაში იქნება გადავარდნილი და მეტაფიზიკური შფოთვების გარდა, მართლა ვერაფერს დავუპირისპირებთ. თუმცა, თუკი გავიხსენებთ როგორ ემყარება ყოველგვარი შეფასება ფარდობითობას და გამოვცვლით იმ საფუძველს, რომელზეც მდგომარეობის აღქმა დავაშენეთ, ანუ ორგანზომილებიანი სივრცის (მაგიდიდან) მაგიერ მოცემულობას შევაფასებთ სამგანზომილებიან სივრცეში, ზემოხსენებული დამზაფვრელად გაურკვეველი განუზღვრელობა პრიმიტიულად ახსნადი, ცხადი და პირდაპირ ხელშესახები გახდება. აღარ დაგვჭირდება მეტაფიზიკური გოდება და იდეალისტური წესრიგის, მისტიკური გნოსეოლოგიური ოპერატორების შემოღება.

ახლა, უსასრულობის ხელშესახები ბუნება უფრო ზუსტად, მათემატიკურად რომ ავხსნათ, ფორთოხლის ალეგორიაზე მსჯელობას მოვეშვათ და მისი ნამდვილი შესატყვისი განვიხილოთ, რასაც სინამდვილეში “რიმანის სფერო” ეწოდება. ამ მათემატიკურ მოდელში წარმოდგენილია ერთეულოვანი სფერო, ცენტრით ათვლის სათავე O – ზე (იხ. ნახაზი 1^[1]), რომელსაც კომპლექსური სიბრტყე შუაზე კვეთს. თუკი კომპლექსური სიბრტყის ნებისმიერი z წერტილიდან სფეროს პოლუს N – ზე გავავლებთ წრფეს, იგი აუცილებლად გადაკვეთს სფეროს რაღაც P წერტილში. თქმული იმას ნიშნავს, რომ არ არსებობს მოცემულ კომპლექსურ სიბრტყეზე რაიმე ადგილმდებარეობა, თუნდაც სფეროსაგან უსაშველოდ შორი, საიდანაც გავლებული წრფე პირდაპირ N წერტილს მიაღწევს, ანუ ყოველთვის გვექნება კონკრეტული კვეთა სფეროს ზედაპირზე.

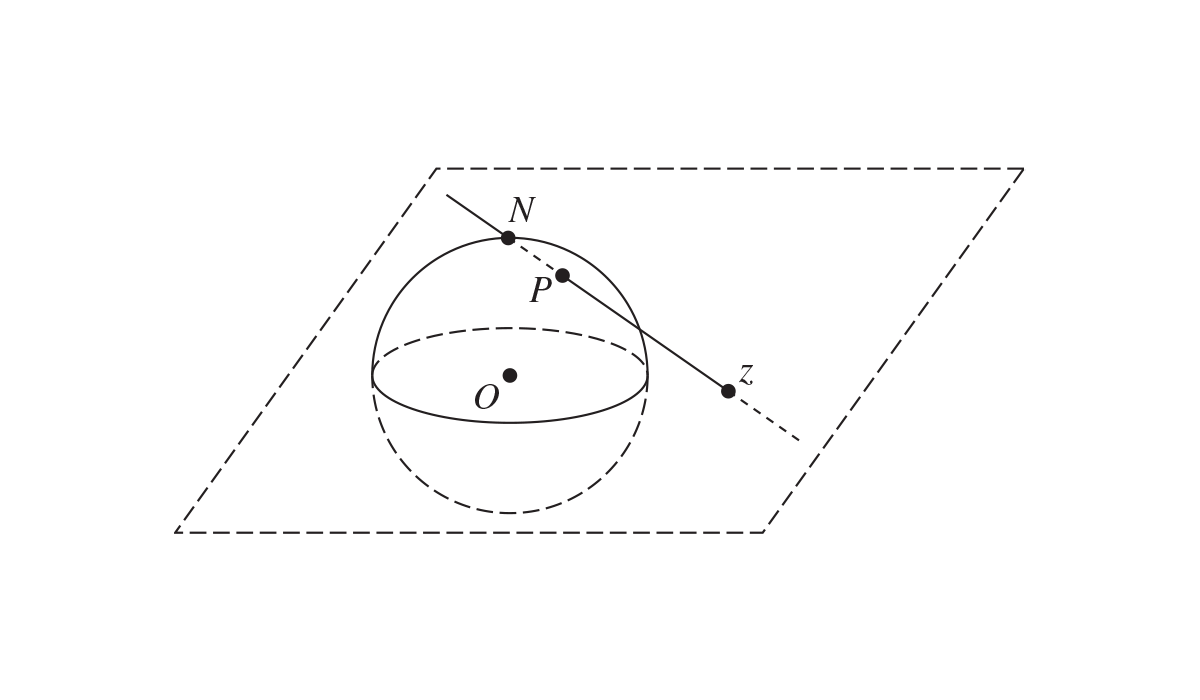
“რიმანის სფეროს” დიდებულება იმაში მდგომარეობს, რომ უსასრულოდ დიდ სიბრტყეზე, უსასრულოდ ბევრ კომპლექსურ რიცხვს ერთ ნაცნობ, გასაგებ, აღწერად გეომეტრიულ ფიგურაში ათავსებს,- სიბრტყის უსასრულოდ ბევრი წერტილიდან ნებისმიერისთვის მოიძებნება შესაბამისობა, უნიკალური წერტილი სფეროზე (კვეთის სახით). ხოლო ზოგადად სიშორე შემოუწერელ, უკიდეო სიბრტყეზე, ანუ ზოგადად მთელი უსასრულობა, წარმოდგება ერთი ცალი ერთეულით, ერთი ცალი წერტილით, სფეროს N პოლუსით. მარტივად რომ ვთქვათ, რიმანის ამ გეომეტრიულ მოდელში, უსასრულობა, როგორც ერთი შეხედვით ამოუწურავი, შეუცნობელი და მიუწვდომელი სიდიდე გადააზრებადია ისეთ ცხად და ნაცნობ მოცემულობად, როგორიც სფეროა; ხოლო ზოგადად მთავარი ბუნდოვანება, განუზღვრელობა, ერთ ცალ წერტილად იქცევა.

მიუხედავად იმისა, რომ მათემატიკური გარდამავლობის თვალსაზრისით, ყველაზე ლოგიკური იქნებოდა განხილულ საკითხზე სულ ბოლოს გვესაუბრა, ჩემთვის მნიშვნელოვანია, მკითხველს დასაწყისშივე წარმოვუდგინო ფიქრის ფარდობითობის გაშინაგნების აუცილებლობის ბრწყინვალე მტკიცებულება. “რიმანის სფერო” აზროვნებისას, ანუ ფარდობითობას დაფუძნებული მოქმედებისას, მოუხერხებლად შერჩეული შეფასებითი საფუძვლით (გნებავთ, ათვლის სხეულის) გამოწვეული ბუნდოვანების პასუხი, მეტაფიზიკური ორომტრიალის დაბეჩავება და ლამაზი მათემატიკური მეტაფორაა.

უსასრულობის ზღვარი

ამ სტატიაში მე ვიმუქრები უსასრულობის ხელშესახები ბუნების წარმოჩენით, ხაზგასმით, რომ ზებუნდოვან მეტაფიზიკურ განუჭვრეტელობასთან კი არა, ხელმისაწვდომ და გამოყენებად, გარემოების აღმწერ არაჩვეულებრივ საშუალებასთან გვაქვს საქმე. მოდი განვიხილოთ, როგორ შეიძლება მათემატიკურ ოპერაციებში უსასრულობის გამოყენება ისეთი ბანალურად საჭირო შედეგების მისაღებად, როგორიც, თუნდაც, წრეწირის ფიზიკური პარამეტრებია.
ყველაფერი მაშინ დაიწყო, როცა კაცობრიობა მიხვდა, რომ სტატიკური (წონასწორობაში მყოფი, გნებავთ – უძრავი) გარემოებების აღწერით ბევრს ვერაფერს მიაღწევდა და მოძრაობით დატენილი არსებობის გასაზომად ისეთი მათემატიკა გვჭირდებოდა, ცვლილებებს რომ აფასებდა. ამიტომაც, თქვეს ისააკ ნიუტონმა და გოტფრიდ ვილჰელმ ლაიბნიცმა,- იყოსო კალკულუსი და იქმნა კალკულუსი.
ჩამოვაყალიბოთ უფრო ცხადად. კალკულუსი ეფუძნება ორ არსებით მათემატიკურ მოქმედებას, გაწარმოებასა და ინტეგრირებას. გაწარმოება ისეთი ოპერაციაა, რომელიც აღწერს ცვლილების მაჩვენებელს, მაგალითად როგორ შეიძლება იცვლებოდეს სხეულის სიჩქარე ან თუნდაც მოსახლეობის რაოდენობა რომელიმე სახელმწიფოში. ინტეგრირება გაწარმოების შებრუნებულია,- გვაქვს ცვლილების მაჩვენებელი და ვსაზღვრავთ იმ გარემოს მოქმედების წესს, რომელმაც ეს ცვლილება გამოიწვია. შესაბამისად, რადგანაც სამყაროს აბსოლუტურად ყველა მდგომარეობაში სიცოცხლის მთავარ მახასიათებელს, – ცვლილებას,- ვხვდებით, კალკულუსი მულტიდისციპლინარული და არსებითი მათემატიკური დარგი გამოდის.

უშუალოდ კალკულუსი, მისი ორივე მთავარი ოპერაცია, ფუნქციის ზღვრის ცნებას ეფუძნება, ხოლო ფუნქციის ზღვრის გამოყენებაში არსებითი უსასრულობის მოცემულობაა. ახლა, ამ უსასრულობის მოცემულობას განვიხილავთ, ავხსნით, როგორ მონაწილეობს ეს უთავბოლო სიდიდე ყველაზე ყოვლისმომცველ, ანუ ცვლილების აღმწერ მათემატიკურ მოქმედებებში. ჩვენ უზოგადესად ვისაუბრებთ ფუნქციის ზღვარზე, მას არ განვმარტავთ სიღრმისეულად, მხოლოდ უსასრულობასთან მიმართებით გავარჩევთ, ფილოსოფიური მსჯელობისთვის სამყოფი ზედაპირულობით რომ გამოერკვეს მკითხველი მის არსში.

ჯერ ზეგამარტივებულად ვთქვათ, რომ ფუნქცია მხოლოდ და მხოლოდ რიცხვზე მოქმედების წესია, მეტი არაფერი. ანუ, თუკი გვაქვს რაღაც ფუნქცია

\(f(x) = x^2 – 1\),

ნიშნავს, რომ ცვლადის ნებისმიერ მნიშვნელობას ჯერ საკუთარ თავზე ვამრავლებთ და შემდეგ ერთიანს ვაკლებთ; ანუ

როცა \(x = 1\), მაშინ \(f(1) = 1*1-1\),

სულ ესაა. თუმცა, ხანდახან ისეთ ფუნქციებსაც ვაწყდებით, როცა ცვლადის რომელიმე მნიშვნელობისთვის მისი განსაზღვრა აღარ გამოგვდის, მაგალითად,

\(f(x) = \frac{x^2 – 1}{x – 1}\)და \(x=1\),

ანუ

\(f(1) = \frac{1*1 – 1}{1 – 1} = \frac{0}{0}\);

ცხადია, ნულს ნულზე ვერ გავყოფთ, არაფრის არაფერზე გაყოფა შეუძლებელია, არაფერი უბრალოდ არაფერია. როცა ასეთ შემთხვევას გადავეყრებით, თუნდაც ჩვენს მაგალითში, ვამბობთ, რომ ფუნქციას აქვს წყვეტის წერტილი (აქ, \(x = 1\)); რაც იმას ნიშნავს, რომ უბრალოდ ვერ მოიძებნება \(f(1)\) მნიშვნელობა. იქიდან გამომდინარე, რომ სამყაროში ყველაფერი მათემატიკური ფუნქციით აღიწერება, მით უმეტეს ცვლილებები, გვჭირდება ხოლმე მათი ბუნების სრულფასოვნად ცოდნა, თუნდაც სწორედ იმ ერთადერთ წერტილთან, როცა განუზღვრელობას ვაწყდებით. ამისათვის არსებობს ფუნქციის ზღვრის ცნება, რაც თავის თავში იმას ნიშნავს, რომ ცვლადის პრობლემურ მნიშვნელობას ვუახლოვდებით და ვუახლოვდებით უსასრულოდ, თუმცა არასოდეს ზუსტად მას არ ვეკარებით, მასთან უსაშველოდ ახლო მიდამოს ვაკვირდებით, ყველა წერტილს მის “სამეზობლოში” იმ ერთი ცალი განუსაზღვრელი წერტილის გამოკლებით და ფუნქციის სახეზე წარმოდგენას ასე ვიქმნით. მაგალითად, ჩვენი ფუნქცია წყდება \(x = 1\) წერტილში, თუმცა შეგვიძლია მისი მნიშვნელობის გამოთვლა \(x =0.9997, x = 0.9998, x =0.9999\) და ა.შ. წერტილებში. ჩამოთვლილი წერტილებისთვის კი ფუნქციის მნიშვნელობები შესაბამისად:

\(f(0.9997) = \frac{0.9997^2 – 1}{0.9997 – 1} = 1.9997\),

\(f(0.9998) = \frac{0.9998^2 – 1}{0.9998 – 1} = 1.9998\),

\(f(0.9999) = \frac{0.9999^2 – 1}{0.9999 – 1} = 1.9999\).

დავაკვირდეთ, რომ რაც უფრო ვუახლოვდებით წყვეტის წერტილს \(x = 1\), ფუნქციის მნიშვნელობა მით მეტად უახლოვდება 2 – ს. ასეთ დროს ვამბობთ, რომ ფუნქციის მნიშვნელობა მიისწრაფვის ორისაკენ (მისი ზღვარია 2) მაშინ, როცა \(x\)მიისწრაფვის ერთისკენ. ესეც ფუნქციის ზღვრის ცნების უზოგადესი შინაარსი. უკვე შეგვიძლია თამამად გადავიდეთ ყველაზე საინტერესო ნაწილზე.

განხილულ მაგალითებში კონკრეტულ ფუნქციებში ცვლადის განსხვავებული მნიშვნელობები შევიტანეთ, სხვადასხვა რიცხვები. ფუნქციებიც მარტივად, ცვლადის ამ მნიშვნელობებს შესაბამისად ექცეოდნენ, მარტივ არითმეტიკულ გარდაქმნებს უტარებდნენ. რა მოხდება, თუ ცვლადის მნიშვნელობად ფუნქციაში არა რომელიმე რიცხვს (1 – ს, 2 – ს, 0.9997 – ს ან თუნდაც 10 000 000 – ს), არამედ უსასრულობას შევიტანთ? უსასრულობა ხომ რიცხვი არაა? პრინციპში, არც არაფერი მოხდება, ფუნქციაში უსასრულობას ვერ შევიტანთ ახლახან კითხვად ჩამოყალიბებული მოცემულობის გამო. სამაგიეროდ შეგვიძლია ფუნქციის ცვლადი ისე მივასწრაფოთ უსასრულობისაკენ, წეღან რომ 1 – სკენ მიისწრაფოდა. ახლა, ავხსნათ, როგორ ხდება ეს.
წარმოვიდგინოთ უმარტივესი ფუნქცია, მაგალითად

\(f(x) = \frac{1}{x}\).

იმისათვის, რომ ამ ფუნქციის ზღვარი გამოვთვალოთ მაშინ, როდესაც \(x\) მიისწრაფვის უსასრულობისკენ, ზუსტად ისე, როგორც წინა მაგალითში, უნდა წარმოვიდგინოთ რომ ცვლადი ძალიან, უკიდურესად უახლოვდება საკუთარ სამიზნეს; ანუ, ფიქრის მიმდინარეობა ზუსტად იგივენაირია,- როცა \(x\) რაღაცისკენ მიისწრაფვის, ამ რაღაცასთან უფრო და უფრო დაახლოებული სიდიდეებისთვის ვაკვირდებით ფუნქციის მნიშვნელობას და სრულიად ფუნქციის ზღვარსაც ასე ვანგარიშობთ. თუმცა რადგან უსასრულობა რიცხვი არაა, ვერ ვიფიქრებთ რამე კონკრეტულ წერტილებზე, რომლებიც მის სამეზობლოშია, მასთან კრიტიკულად ახლოსაა. ამის მაგიერ, უსასრულობა გაიაზრება როგორც უზარმაზარი, უსაშველოდ დიდი მნიშვნელობა.

ამ დროს სწორედ უკვე მრავალჯერ ნახსენები ფიქრის განმსაზღვრელი სიდიდე, ფარდობითობა გამოდის ასპარეზზე – ჩვენი “ათვლის სხეული” ერთიანია, ფუნქციის წილადის მრიცხველი. თუ უსასრულოდ დიდ სიდიდეს ერთიანთან დადარებით გავიაზრებთ, ძალიან მარტივია იმის თქმა, რომ ერთიანი უსასრულოდ დიდი ზომის რიცხვთან შედარებით აბსოლუტურად უმცირესია. ყველამ ვიცით, რაც უფრო დიდ რიცხვზე გავყოფთ ერთიანს, შედეგი მით უფრო პატარა იქნება (ერთის 2-ზე გაყოფისას 0.5 – ს ვიღებთ; 20 – ზე გაყოფისას – 0.05 – ს; 20 000 – ზე გაყოფისას – 0.00005 – ს და ა.შ.). ამიტომ, მისი უსასრულოდ უზარმაზარ მნიშველობაზე გაყოფისას შედეგი ნულს დაუხალოვდება. მოკლედ, გამოდის, რომ როდესაც მიისწრაფვის უსასრულობისკენ, ჩვენი სამაგალითო ფუნქცია უახლოვდება ნულს, ფუნქციის ზღვარი ნულია. სხვათა შორის, ზუსტად იმავენაირი წარმატებით შეგვიძლია, ფუნქციის ცვლადი მინუს (უარყოფით) უსასრულობაში მიისწრაფოდეს. ამ შემთხვევაში, უბრალოდ, უსაშველოდ დიდი სიდიდის მაგიერ, უსაშველოდ მცირე სიდიდე უნდა წარმოვიდგინოთ, დანარჩენად ყველაფერი იგივეა.

არ მინდა, რომ მკითხველისათვის ზღვარში უსასრულობის გამოყენება ისეთ აბსტრაქტულ და ყოვლადგამოუყენებელ ლაყბობად დარჩეს, როგორიც მეტაფიზიკური ტრაქტატებია ხოლმე. ამისთვის სტატიის მოცემული თავის შესავალში ნახსენები პრიმიტიული მაგალითივე განვიხილოთ, მათემატიკური ზღვრის კონკრეტული ბუნებისა და ხელშესახები გამოყენებითობის ნათელსაყოფად. ვისაუბროთ წრეწირზე. ასეთი ცხადი, საყოველთაო და კონკრეტული გეომეტრიული ფიგურის ფართობის დათვლა, სწორედ ზღვრების, ხსენებული უსასრულობისაკენ სწრაფვის გამოყენებით გახდა შესაძლებელი. წარმოიდგინეთ, მათემატიკური ზღვრის იდეის გარეშე წრეწირების ფართობის ზუსტად გამოანგარიშება კაცობრიობას არ შეეძლო. დავაკვირდეთ წარმოდგენილ ნახაზს^[2].

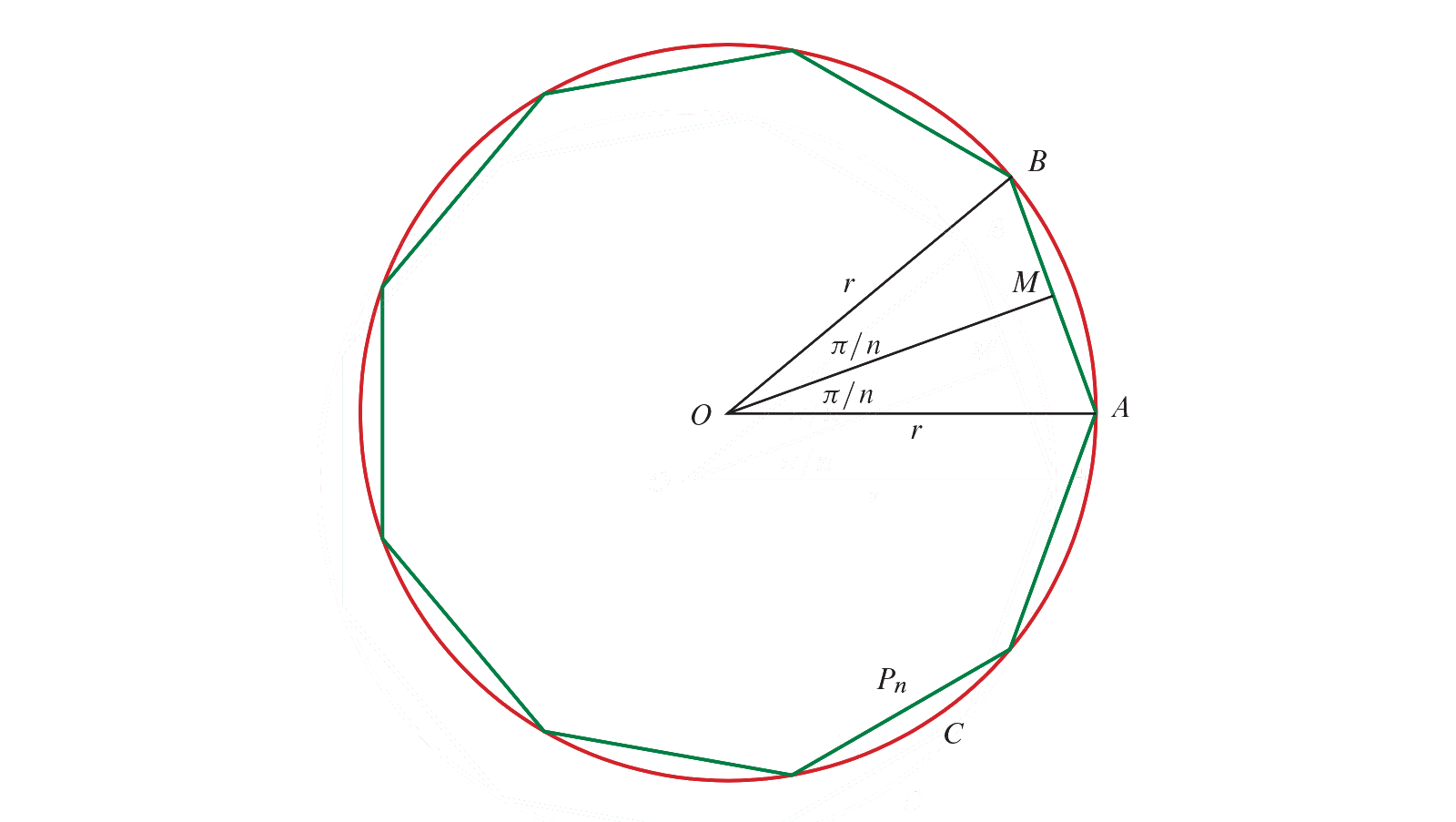
ის წრეწირი, რასაც ხედავთ, კომპიუტერმა დახაზა. იცით როგორ ხაზავენ წრეწირს კომპიუტერები? სინამდვილეში ესაა წესიერი (ტოლი გვერდების მქონე) მრავალკუთხედი, რომელსაც 180 გვერდი აქვს (გნებავთ, ასოთხმოცკუთხედი), 180 გვერდი კი იმდენად ბევრია, რომ თვალისათვის შეუძლებელია იდეალური წრეწირისაგან მისი გამორჩევა. ზოგადადაც, წრეწირის ფართობი ასე იანგარიშება ხოლმე, წარმოიდგენენ წესიერ მრავალკუთხედს, რომლის გვერდებსაც აერთებენ მრავალკუთხედის ცენტრთან და იღებენ იმდენ სამკუთხედს, რამდენი გვერდიც აქვს მრავალკუთხედს (კომპიუტერის შემთხვევაში 180 სამკუთხედს). სამკუთხედის ფართობის დათვლა მარტივი გეომეტრიის ნაწილია, წრეწირისაგან განსხვავებით ინტუიციურიც. ამ დროს, თუკი წესიერი მრავალკუთხედის გვერდების რაოდენობას n – ით აღვნიშნავთ და დავწერთ n ცალი სამკუთხედის ფართობთა ჯამის ფორმულას, ხოლო n – ს მივასწრაფებთ უსასრულობისკენ (ზუსტად ისე, როგორადაც ახლახან განხილული ფუნქციის მაგალითში), წრეწირის ფართობსაც მივიღებთ. ანუ, თუკი უსასრულოდ ბევრი გვერდის მქონე წესიერ მრავალკუთხედს განვიხილავთ, სინამდვილეში, საუბარი წრეწირზე გამოგვდის და რადგანაც მრავალკუთხედის ფართობის დათვლა (მასში ჩახაზული სამკუთხედების ფართობის ცოდნის გამო) მარტივად შეგვიძლია, წრეწირის ფართობსაც დავთვლით.

უკვე საკმარისი ცნებითი საფუძველი შევქმენით იმისათვის, რომ კალკულუსში უსასრულობის ბუნებას დავაკვირდეთ. პირველ მაგალითში, როდესაც ფუნქციის წყვეტის წერტილს ვიკვლევდით, მას ვუახლოვდებოდით უსასრულოდ, რაც იმას ნიშნავდა, რომ გზას იმ წერტილამდე ათასებად, ათი ათასებად, მილიონებად, დეცილიონებად ვშლიდით, მივემართებოდით მისკენ უსასრულოდ, თუმცა არასოდეს ვაღწევდით ან ვცდებოდით მას; ანუ ამ გზაზე სვლას ჰქონდა რაღაც მტკიცედ გამოხატული ფორმა, წესი და საზღვარი, იყო გააზრებადი და კონკრეტულად მოპყრობადი. მეორე შემთხვევაში, როცა ცვლადს უსასრულობისკენ მისწრაფებისას განვიხილავდით, უსასრულობა იყო სიდიდის იდეალი, მართალია შემოუსაზღვრავი და კონკრეტულად მოუცემელი, მაგრამ ჭვრეტადი და გამოყენებადი, ბოლოს და ბოლოს ერთიანი მასთან მიმართებაში შევკვეცეთ. თუკი დავაკვირდებით, კალკულუსში უსასრულობა გამოდის ერთგვარი მიმართული მიმდინარეობა, არა კონკრეტული მონაცემი. ესაა ცნობიერი სწრაფვა, ცნობიერი რადიკალური ზრდა ან ცნობიერი რადიკალური კლება.

უმნიშვნელოვანესია, რომ უსასრულობის კალკულუსისებრი გაგება ცნებას აცლის მეტაფიზიკური ბუნდოვანების საბურველს. კი, იგი კლასიკური გაგების ყალიბშია, – არის მიუწვდომელი და შემოუსაზღვრავი,- თუმცა, იმის გამო, რომ მონაცემი კი არა, გააზრებადად მიმართული მიმდინარეობაა, გაურკვევლობას აღარ მოასწავებს. პირიქით, გვეხმარება ჩვენს გარემოში მოცემულის გაურკვეველი ბუნების ამოსაცნობად, შესასწავლად და შესაფასებლად (მაგალითად როგორი ფორმა ექნება ფუნქციის გრაფიკს, როცა მისი ცვლადი გაიზრდება და გაიზრდება გაუჩერებლად, ან რა იქნება იდეალური სიმრუდის ფართობი). უსასრულობა გამოდის კონკრეტული სწრაფვა აბსტრაქტულისკენ, ხიდი უსასრულობასა და სასრულობას შორის. ამ უკიდეო ცნების “მორჯულება”, მათემატიკურ ოპერაციებში გამოყენება იმისათვის, რომ გარესამყარო, ზოგადად ცვლილებები აღიწეროს, ხელშეუხებელ და შფოთიან მოცემულობას აქცევს ხელმისაწვდომად, გასაგებად.

როგორ ავჯამოთ უსასრულობა

თხრობა დავიწყოთ ადამიანთა და კუთა ყველაზე ცნობილი დაპირისპირებით. საკუთარი გონებამახვილობის საყოველთაო ენაზე ამოსაწერად, ზენონ ელეელმა, როგორც პოპვარსკვლავი ფიზიკოსების პირველმა წინაპარმა, აღგვიწერა^[3]  მდგომარეობა, როდესაც ათლეტობის იდეალი, ღმერთკაცი აქილევსი კუს სირბილში შეეჯიბრა. იმისათვის, რომ კუ არათანაბარ მდგომარეობაში არ აღმოჩენილიყო, ფორა მისცეს, სირბილი მან წინსწრებით დაიწყო. ზენონი ამტკიცებს, რომ აქილევსი კუს ვერასოდეს გადაასწრებს, რადგანაც:

1. კუს რომ დაეწიოს, ჯერ ის მანძილი უნდა გაირბინოს, საიდანაც კუმ მოძრაობა დაიწყო.
2. როცა აქილევსი ამ ადგილს მიაღწევს, ამასობაში კუს რაღაც ახალი მანძილი ექნება გავლილი.
3. ახლა აქილევსს გადასასწრებად ამ დამატებული გზის გარბენა მოუხდება, თუმცა როცა შეძლებს, კუ ისევ წინ იქნება წასული.
4. ეს მდგომარეობა გაგრძელდება უსასრულოდ,- რამდენჯერაც აქილევსი იმ ადგილთან მიირბენს, სადაც მეტოქე იყო, ამ დროში კუ ისევ ახალ მანძილს დაფარავს.

მოკლედ, ზენონმა ჩამოგვიყალიბა მდგომარეობა, სადაც სინამდვილე გატეხილია და ყველანი უსასრულო წრებრუნვაში ვიჭედებით, როცა, მაგალითად, პურის საყიდლად მივდივართ,- მაღაზიამდე მისასვლელად ჯერ გზის ნახევრის გავლა მოგვიხდება; როცა გავივლით, დარჩენილის ნახევარი უნდა გავიაროთ; ამასაც რომ მივაღწევთ, ნახევრის ნახევარი და ა.შ. გზის განახევრება არასოდეს დასრულდება და უპუროდ დავრჩებით.

ზენონის პარადოქსები, ერთი შეხედვით, უსასრულობის გაუგებარი ბუნების მეტაფიზიკურ ძეგლს აგებს და ისტორიულად, ბევრ მოაზროვნესაც ცრიდა წელში, როცა მათ გადაჭრას აბსტრაქტული ცნებებით ცდილობდა. თუმცა, როგორც უკვე წინა თავში ვახსენეთ, კაცობრიობამ მოახერხა კალკულუსამდე განვითარება და აღმოაჩინა ასეთი რამ,- თურმე არსებობს უსასრულო ჯამები, რომელთა შედეგებიც ასე სულ კი არ იზრდება და იზრდება, არამდე ერთ კონკრეტულ რიცხვამდე იკრიბება. პრინციპში, ფაქტი, რომ პურის შეძენას ადამიანები კალკულუსის გამოგონებამდეც ახერხებდნენ, როგორღაც ისედაც ხსნის სიდიდის უსასრულოდ ბევრ დისკრეტულ ელემენტებად გახლეჩის არც ისე ჩახლართულ ბუნებას, თუმცა, მათემატიკური რუდუნებითაც გავაანალიზოთ, როგორი კონკრეტული და ხელშესახებია ზემოხსენებული ელინური მღელვარება.

დავუშვათ, კუმ სირბილი აქილევსისგან დაშორებით, რაღაც \(d\) მანძილზე დაიწყო (ფორა, რომელიც ზენონმა წინაპირობად შემოიღო). ვთქვათ, არც აქილევსი იყო ძალიან ღმერთკაცი და არც კუ ყოფილა ერთმნიშვნელოვნად კუ,- მივიჩნიოთ, რომ გმირი მხოლოდ ორჯერ სწრაფი იყო მეტოქეზე. ეს იმას ნიშნავს, რომ როცა აქილევსი \(d\) მანძილს გაირბენდა, ამ დროში კუ \(\frac{d}{2}\)– ს გაივლიდა. ესე იგი:

1. თავიდან, აქილევსს დასაფარი აქვს \(d\) გზა, სანამ მოახერხებს, ამასობაში კუ \(\frac{d}{2}\) გაივლის.
2. ახლა, აქილევსს უწევს გაირბინოს \(\frac{d}{2}\), რა დროშიც კუ დამატებით \(\frac{d}{4}\)– ით გადაადგილდება.
3. აქილევსის გასავლელი მანძილი \(\frac{d}{4}\) გახდა, კუმ კი წინ კიდევ \(\frac{d}{8}\)– ით წაიწია.
4. ასე გრძელდება უსასრულოდ.

ახლა, თუკი აქილევსის ჯამურ გავლილ მანძილს აღვნიშნავთ \(S\)– ით, გამოვა, რომ

$$S = d + \frac{d}{2} + \frac{d}{4} + \frac{d}{8} + \dots$$

თუ დავამტკიცებთ, რომ აქილევსის გავლილი მანძილი (\(S\)) სასრულია, გამოვა, რომ ოდესღაც ეს სირბილი დამთავრებულა, კუსაც დასწევია და რახან უფრო სწრაფია, გადაასწრებდა კიდევაც.

მოცემულ უსასრულო ჯამს მათემატიკაში გეომეტრიული პროგრესია ჰქვია და წინა თავში ახსნილი საკითხის, ფუნქციის ზღვრის ცნების პირდაპირი გაგრძელებაა. საყოველთაოდ ცნობილი ფორმულაც არსებობს მისი მნიშვნელობის პირდაპირ გამოსათვლელად, მაგრამ რადგანაც პირობა დავდე, ნებისმიერი მიმართულების სპეციალისტისათვის თხრობა გასაგები იქნებოდა და საჭიროებაც არ არის, უცხო მათემატიკური განტოლებები ვწერო, \(S\)– ის მნიშვნელობას პატარა ალგებრული მანიპულაციით გამოვთვლი:

უკვე შევთანხმდით, რომ გვაქვს \(S = d + \frac{d}{2} + \frac{d}{4} + \frac{d}{8} + \dots\);

შემოვიღოთ რაღაც \(r\), რომელიც რიცხობრივად იმის ტოლია, რამდენჯერაც ყოველი მომდევნო გასავლელი მანძილი მცირდება, ანუ

\(r = \frac{1}{2}\);

თუკი \(S\)– ს გავამრავლებთ \(r\)– ზე:

\(S \cdot r = \left(d + \frac{d}{2} + \frac{d}{4} + \frac{d}{8} + \dots \right) \cdot r\)

ანუ

\( \frac{S}{2} = \left(d + \frac{d}{2} + \frac{d}{4} + \frac{d}{8} + \dots \right) \cdot \frac{1}{2} = \frac{d}{2} + \frac{d}{4} + \frac{d}{8} \dots\)

რატომღაც \(S\) – ს გამოვაკლოთ \(\frac{S}{2}\):

\( S – \frac{S}{2} = \left(d + \frac{d}{2} + \frac{d}{4} + \frac{d}{8} + \dots \right) – \left(\frac{d}{2} +
\frac{d}{4} + \frac{d}{8} + \dots \right) = \)

\(= d + \left(\frac{d}{2} + \frac{d}{4} + \frac{d}{8} + \dots \right) – \left(\frac{d}{2} + \frac{d}{4} +
\frac{d}{8} + \dots \right) = d\)

ანუ

\(\frac{S}{2} = d\)

და

\(S = 2 \cdot d\)

როგორც აღმოჩნდა, \(S\), ანუ აქილევსის გავლილი მანძილის აღმწერი უსასრულო ჯამი რაღაცის ტოლია, სასრული მნიშვნელობისაა და მეტიც, \(2*d\)– ს უდრის. ანუ ჩვენი შემოღებული პირობებით (როცა აქილევსი კუზე ორჯერ სწრაფია) გმირი მეტოქეს დაეწევა მაშინ, როდესაც \(2*d\) სიგრძის მონაკვეთს გაირბენს.

ზენონის პარადოქსს მათემატიკურად ვუპასუხეთ და ამაზე უფრო მეტის თქმაც მინდა, მაგრამ მანამდე, უმჯობესი იქნება უსასრულო ჯამის კიდევ ორ მაგალითსაც თუ განვიხილავთ. ნასაუბრებ ამოცანაში, ასე თუ ისე, ბევრი პირობაა,- ორი მორბენალი, ორი ცვლადი, ათასი ლაყბობა, – მე კი მინდა საკითხი ელემენტარულ ნაწილაკებამდე გავამარტივო. ამიტომაც, ახლა ვაჩვენებთ, რომ უსასრულო პერიოდული ათწილადი 0.999…, ანუ დაუსრულებელი ჩანაწერის მქონე რიცხვი (რომელშიც ცხრიანი უბოლოოდ იწერება), ერთის ტოლია. მაშასადამე,

უნდა დავამტკიცოთ, რომ

\(0.999\ldots = 1 \).

ვთქვათ, რომ \(x = 0.999\ldots\) და ამ ტოლობის ორივე მხარე გავამრავლოთ 10 – ზე:

\(10x = 10\cdot 0.999… = 9.999\ldots\)

ტოლობის ორივე მხარეს გამოვაკლოთ \(x\):

\(10x – x = 9.999\ldots – x\)

ანუ

\(10x – x = 9.999\ldots – 0.999\ldots\)

მივიღებთ, რომ

\(9x = 9\)
\(x = 1\)

და რადგანაც \(x = 0.999\ldots\), გამოდის, რომ

\(0.999\ldots = 1\)

პირობა დამტკიცებულია და აქვე, ისიც გავითვალისწინოთ, რომ მოცემული პერიოდული ათწილადი ჯამის სახითაც ჩაიწერება:

\(0.999\ldots = 0.9 + 0.09 + 0.009 + 0.0009 + \dots = 1\)

თუკი ზენონის მსჯელობაში ან ჩემს მაგალითში რამენაირად პარადოქსული ბუნება შეიმჩნევა, ამის პასუხი ისევ მრავლადნახსენები ფიქრის ფარდობითობაა,- აზროვნების მიმდევრობას არასწორ ფუძეზე ვაგებთ, მდგომარეობას ცუდად შერჩეულ წინაპირობას, (ათვლის სხეულს) ვადარებთ. აი, თავიდან ზენონი პარადოქსების წერისას, შემდეგ კი დისკრეტული მათემატიკის პირველ ლექციაზე შესული ყველა დაბნეული სტუდენტი გაოცებისას, იმას ვერ ითვალისწინებდნენ, რომ უსასრულობის ბუნება არ არის მატერიალური, მატერიალური სამყაროს მახასიათებლებით რომ შეაფასო, აბსტრაქციაა და მხოლოდ ადამიანის გონებაში არსებობს. ანუ, როდესაც უსასრულობანარევ მათემატიკურ ამოცანაზე მსჯელობ და ამასობაში, უსასრულობას ისე უდგები, როგორც ფიზიკურ, შეგრძნებით სამყაროში დამზერილ მონაცემს ან გარემოებას, ვერაფერს ვერ ამოხსნი და გადაწყვეტ, რომ პარადოქსი აღმოაჩინე. ძალიან მარტივად, როცა 0.9 – დან 1 – მდე სვლას განიხილავ, ისე არ უნდა იფიქრო, როგორც სახლიდან მაღაზიაში (პურის საყიდლად) წასვლაზე ან როცა სირბილში შეჯიბრებას უკირკიტდები, მოვლენას ისე ვერ შეაფასებ, როგორადაც რიცხვთა ღერძის მიმდევრობას.

უსასრულობის ბუნების, როგორც მათემატიკური აზრის აბსტრაქციის გააზრებისას, შეგვიძლია დავფიქრდეთ სხვა მათემატიკური აზრის აბსტრაქციის, რიცხვების, სახეზე. მატერიალურ სამყაროში არ არსებობს ერთიანი, ორიანი ან ცხრიანი. ჩვენ შეგვიძლია ფურცელზე დავწეროთ მათი აღმნიშვნელი სიმბოლო ან მივუთითოთ რაოდენობაზე,- მაგალითად ერთი ვაშლატამა, ორი აგური, ცხრა ფოსტალიონი,- მაგრამ მატერიალურად წარმოდგენილ ერთიანს, ორიანს, ცხრიანს ვერსად შევხვდებით. ამის მიუხედავად, რიცხვებს, როგორც აბსტრაქციებს, თავიანთი არსებობის წესრიგი აქვთ და აბსოლუტურად ნებისმიერ ფიზიკურ მონაცემს შეგვიძლია მივუსადაგოთ, მათით გამოვსახოთ, აღვწეროთ და კიდევ უფრო გადასარევი, შევიმეცნოთ. ასეა უსასრულობაც, არის აბსტრაქცია და აქვს თავისი კანონზომიერებაც, რომლითაც, სხვათა შორის, ათასი მოვლენა შეგვიძლია შევისწავლოთ.

სასრულ სიდიდემდე შეკრებადი უსასრულო ჯამების ბუნებაც ასეთია. ზუსტად ისე, როგორც მათემატიკურ ზღვარში, უსასრულობა მიმდინარეობაა და არა დანიშნულების წერტილი, მისამართი. კიდევ გავიხსენოთ, რაზე ვსაუბრობთ,- ამ ჯამებში რიცხვები ერთმანეთს ემატება და ემატება და ამასთან, ყოველი მომდევნო შესაკრები წინაზე უფრო მცირეა. ვინაიდან რიცხვებს ექსტრემუმები არ გააჩნია (ანუ იმდენად პატარა რიცხვი არსებობს, რამდენიც მოგვეხუშტურება), დგება მდგომარეობა, როცა ისეთ მცირე მნიშვნელობებს ვკრებთ, რომ მათ შინაარსი აღარ აქვთ, რაღაცაზე მათი დამატება აღარაფერს ცვლის და ეს ჯამიც კონკრეტულ, სასრულ მნიშვნელობას იღებს. მოკლედ, რაღაც მომენტში, როცა ასეთ ჯამში შესაკრებები აბსურდულად შემცირდება, გინდა დაუმატე და გინდა არა, კონკრეტულ რიცხვს ვეღარ გაცდები.

ავხსნათ განსხვავებულად, ტრაგიკული მარგინალიზმით და ეს იქნება ჩვენი უკანასკნელი მაგალითი. წარმოვიდგინოთ, რომ უფალი კეცავს თაბახის ფურცელს. ჯერ ერთხელ გადაკეცა შუაზე და ფურცლის ზომა განახევრდა, შემდეგ მეორეჯერ, მესამეჯერ, მეოთხეჯერ და რადგანაც ღმერთია, ყოვლისშემძლე მარჯვენის პატრონი, წესით შესქელებული ქაღალდის სიმტკიცე ხელს არ შეუშლის, დაუსრულებლად რომ გააგრძელოს ეს საქმე. მიუხედავად იმისა, რომ ფურცელი უკიდურესად პატარავდება და პატარავდება, მაინც, როცა კი მას გაშლის, თუნდაც მარადისობის შემდეგ, ქაღალდის ზომა ზუსტად იგივე იქნება, რაც თავიდან იყო.

მოკლედ, ფაქტი, რომ რაღაც აბსოლუტურად მცირე მდგენელებად დავყოთ, რომ 0-დან 1-მდე სულ ჩავატევთ წინაზე უფრო მცირე რიცხვს, არ ნიშნავს რომ მთელი არ არსებობს, არ ნიშნავს რომ ერთი არ არსებობს. სინამდვილეში, დღის ბოლოს, ეს უსასრულო შემცირების გზა 0-დან 1-მდე, საზღვრებს ატარებს, რომელშიც სულ იქნება და მათი კონკრეტულობის, განსაზღვრულობის, ხელშესახებობის მოლანდებას ყველაზე გადარეული პოეზიითაც ვერ გაექცევა.

ზოგადად, უსასრულო ჯამები დასამზერად უსაშველოდ შთამბეჭდავია,- ვხედავთ, როგორ შეიძლება დაუსრულებლად შეკრიბო რიცხვები და მაინც რაღაც კონკრეტული მნიშვნელობა მიიღო. ესაა შემთხვევა, როცა დაუსრულებელ მოქმედებას, სრულმნიშვნელოვან უწყვეტობას, მაინც აქვს ხელშესახები, ცხადი კიდე.

დატოლებადი უსასრულობები და მათი არითმეტიკა

წინა თავში უსასრულობა და რიცხვები ერთმანეთს შევადარეთ, როგორც არამატერიალურად მოცემული სიდიდეები, როგორც მათემატიკური აზრის აბსტრაქცია. საინტერესო ისაა, რომ რიცხვები დღის ბოლოს რიცხვებია და რასაც არ უნდა აღწერდნენ, ხეზე ჩამომსხდარი ჩიტების ანათვალს თუ რეაქტიულ მოძრაობას, ყველგან გაიაზრებიან და მოქმედებენ ერთნაირად. მათემატიკური უსასრულობა უფრო მრავალმხრივია, განსხვავებული მიმართებითი სისტემები აქვს და ახლა, სწორედ ერთ-ერთს განვიხილავთ,- ზღვრის შემდეგ ვისაუბრებთ უსასრულო სიმრავლეებზე.

თავიდან, ვთქვათ, რომ სიმრავლე არის ის, რაც შეიძლება იყოს ცარიელი ან სავსე. სიმრავლეები შეიცავენ ან არ შეიცავენ ელემენტებს. იმ სიმრავლეს, რომელიც ელემენტებს არ შეიცავს, ასე მარტივად, ცარიელი სიმრავლე ეწოდება. შეგვიძლია არაცარიელი სიმრავლის ათასი მაგალითი ჩამოვთვალოთ, მაგალითად ჟანგბადის მოლეკულაში (O2) ატომთა ორელემენტიანი სიმრავლე, ქართული ანბანში ასოების ოცდაცამეტელემენტიანი სიმრავლე, ფიფქიას ზღაპარში ჯუჯების შვიდელემენტიანი სიმრავლე და ა.შ.. საგულისხმოა, რომ არსებობს უსასრულო ელემენტების მქონე სიმრავლეებიც, მაგალითად ნატურალურ რიცხვთა ℕ^[4] სიმრავლე.

ზემოთ ჩამოთვლილ ყველა არაცარიელ სასრულ სიმრავლეს აქვს ზომა და მის დასადგენად ელემენტების რაოდენობის დათვლა კმარია,- ჟანგბადის მოლეკულაში ატომების სიმრავლის ზომაა 2, ქართულ ანბანში ასოების სიმრავლის ზომაა 33, ფიფქიას ზღაპარში ჯუჯების სიმრავლის ზომაა 7. რადგან სასრულ სიმრავლეებს ცხადი ზომები აქვთ, მარტივი მოსასაზრებელია, რომ შეიძლება მათი ერთმანეთზე დადარება; ჩვენს მაგალითებში ყველაზე დიდი სიმრავლე ქართული ანბანის ასოებისაა, ყველაზე პატარა – ჟანგბადის მოლეკულის ატომებისა.

ლოგიკურია, რომ უსასრულო სიმრავლეებიც შეიძლება იყოს თვლადი. ზოგადად თვლა ხომ მხოლოდ რიგითობის შესაბამებაა, ანუ თუკი შეგიძლია სიმრავლეში ელემენტებს გადაჰყვე და ჩამოთვალო მერამდენეა, სასრულობისა და უსასრულობის განურჩევლად, ტექნიკურად, თვლადი მაინც იქნება. აქ საგულისხმო მხოლოდ ისაა, რომ უსასრულო სიმრავლეების ზომის შესაფასებლად, ცხადია, მისი ელემენტების დათვლა გამოსავალი არ არის.

საბედნიეროდ 1845 წელს დაიბადა გეორგ კანტორი, რომელმაც უსასრულო სიმრავლეთა გაზომვის გზა მონახა. უპირველესად, კანტორი დაფიქრდა უსასრულო სიმრავლეების ზომათა დადარების კანონზომიერებაზე. ცხადია, ასეთი რამისათვის ყველაზე ადვილი ორ განსხვავებულ სასრულ სიმრავლეზე დაკვირვებაა: ვთქვათ, გვაქვს ორი სასრული, ხუთელემენტიანი სიმრავლე A და B. A სიმრავლის ელემენტებია ასოები {a, b, c, d, e}, ხოლო B სიმრავლის – ციფრები {5,8,1,3,6}. კანტორმა, ძალიან მარტივად, დათქვა, რომ თუკი ორ სიმრავლეს შორის შესაძლებელია ურთიერთცალსახა შესაბამისობის^[5] განსაზღვრა, მაშინ სიმრავლეები ტოლია:

\begin{matrix}
\textit{A}: & a & b & c & d & e \\
& \Updownarrow & \Updownarrow & \Updownarrow & \Updownarrow & \Updownarrow \\
\textit{B}: & 5 & 8 & 1 & 3 & 6
\end{matrix}

 ^[6]

წარმოდგენილი ორი სიმრავლისათვის, ურთიერთცალსახა შესაბამისობა განისაზღვრება შემდეგნაირად: A სიმრავლის თითოეული ელემენტი შეესაბამება B სიმრავლის კონკრეტულ ელემენტს და პირიქით, B სიმრავლის თითოეული ელემენტი შეესაბამება A სიმრავლის კონკრეტულ ელემენტს. ასე, ამ უმარტივესი დაკვირვებით ჩამოყალიბდა წესი, რომელიც ორი სიმრავლის ზომას ერთმანეთს ისე ადარებს, რომ საერთოდ აღარ გვჭირდება მისი ელემენტების დათვლა. შესაბამისად, არსებითი პრობლემა, უსასრულო სიმრავლეების ზომის შეფასების შეუძლებლობა დათვლის მეთოდით, გადაიჭრა.

უფრო მეტად ნათელყოფისთვის, ვიმსჯელოთ ორ უსასრულო სიმრავლეზე, ნატურალურ რიცხვებისა (1,2,3,4,5,6,…) და ლუწი რიცხვებისა (2,4,6,8,10,12,…). სიმრავლეთა ზომების დადარების კანტორისეულმა ხერხმა, ურთიერთცალსახა შესაბამისობის პოვნამ, აჩვენა, რომ ზემოხსენებული ორი სიმრავლე ზომით ტოლია. დავაკვირდეთ გამოსახულებას:

 ^[7]

ძალიან მარტივად,- ერთიანი შევუსაბამეთ ორიანს, ორიანი შევუსაბამეთ ოთხიანს, სამიანი შევუსაბამეთ ექვსიანს და ა.შ.. იმის მიუხედავად, რომ მთელ რიცხვთა სიმრავლისგან განსხვავებით, ლუწ რიცხვთა სიმრავლეს, თითქოს, ნაკლები ელემენტები აქვს (კენტი რიცხვები მასში არ არის), მაინც ამ ორს შორის ურთიერთცალსახა შესაბამისობა არსებობს, ანუ სიმრავლეები ზომით ტოლია.

როდესაც კანტორმა ორი უსასრულო სიმრავლის ზომის შედარების ხერხი შექმნა, მარტივად დაამტკიცა, რომ ნატურალურ რიცხვთა ℕ სიმრავლე რაციონალურ რიცხვთა ℚ^[8] სიმრავლის ტოლიცაა. ამის შემდეგ ინტუიციურად მიიჩნია, რომ ნამდვილ რიცხვთა ℝ^[9]  სიმრავლეც იგივე ზომის უნდა ყოფილიყო, მაგრამ ყველა გონებამახვილური მცდელობის მიწურულს, სიმრავლეთა შორის ურთიერთცალსახა შესაბამისობა ვერ მონახა. ამ მცდელობებში, კანტორმა შეიმუშავა ცნობილი “დიაგონალური არგუმენტი”^[10], რომელზეც არ დავწვრილმანდებით, რადგან ჩვენს თხრობას ჩახლართული მათემატიკური ოპერაციებით დაამძიმებს. მოკლედ რომ ვახსენოთ, “დიაგონალური არგუმენტი” ამტკიცებს, რომ მნიშვნელობა არა აქვს, რა წესით ჩამოწერ ნამდვილ რიცხვებს, როგორ გადაალაგ-გადმოალაგებ, მათი ნაწილი აუცილებლად გამოგრჩება და შესაბამისად, ნატურალურ რიცხვებსაც ვერ შეუსაბამებ. მოკლედ, აღმოჩნდა, რომ რაციონალურ რიცხვთა სიმრავლე ზომით მრავალჯერ აღემატებოდა ნატურალურ რიცხვთა ℕ სიმრავლეს, რაც იმას ნიშნავდა, რომ ერთმანეთისგან განსხვავებული ზომის უსასრულობები არსებობდა და 1874 წელს მათემატიკის სამყარო გადატრიალდა.
უსასრულობას ჩამოეშალა ერთმნიშვნელოვანი არსი. თურმე უსაწყისობა და უბოლოობა, მარადიული განშლადობა, დაუსრულებლობა, სულაც არ არის იდეალური, მისი მრავალი განსხვავებული სახე არსებობს, ერთი მეორეზე დიდია, მეორე – მესამეზე და ა.შ.. ისე, საინტერესოა უსასრულობის ამ მახასიათებელს მეტაფიზიკაში თუ განვაზოგადებთ, რა გამოგვივა; რომ აბსოლუტური იდეალი არ არსებობს და ისიც, რაც წინაპირობად, უზენაესობად, ჩვენი დისკრეტული სამყაროს შებრუნებულად მიგვაჩნდა, პასუხგაუცემელი კითხვების ან დახარვეზებული ფიქრის დინების შვებად რომ შევთითხნეთ, არც ისეთი ერთადერთია, ჩვენსავით ვიღაცაზე პატარაა, ვიღაცაზე დიდია.

კარდინალური არითმეტიკა

უკვე განვიხილეთ, რომ სასრული და უსასრულო სიმრავლეების ზომები განსხვავებულად დაიმზირება. ამის გამო, შემოღებულია სიმრავლის ზომის განზოგადებულად აღმწერი ტერმინი – კარდინალური რიცხვი. ყოველ ჯერზე, როცა კი სიმრავლეთა ზომა ვახსენე, საუბარი იყო კარდინალურ რიცხვზე.
სასრული სიმრავლეებისთვის კარდინალური რიცხვი, ჩვეულებრივად, მასში შემავალი ელემენტების რაოდენობის ტოლია,- ჟანგბადის მოლეკულაში ატომების სიმრავლის კარდინალობაა 2, ქართულ ანბანში ასოების სიმრავლის კარდინალობაა 33, ფიფქიას ზღაპარში ჯუჯების სიმრავლის კარდინალობაა 7.
უსასრულო სიმრავლეებისთვის კარდინალებს საკუთარი სიმბოლური აღნიშვნები აქვთ, რადგან, უსასრულობის რიცხვად მოცემა შეუძლებელია. მაგალითად, ნატურალურ რიცხვთა ℕ სიმრავლის კარდინალი აღინიშნება ℵ0 – ით.
ამ ცოდნით აღჭურვილებმა ვისაუბროთ უმარტივეს ოპერაციაზე, სახელწოდებით სიმრავლეთა გაერთიანება. როცა ორ სიმრავლეს ვაერთიანებთ, ვიღებთ ახალ სიმრავლეს, რომელიც წინა ორის ელემენტებს ერთად შეიცავს (ძალიან ჰგავს ჯამს და მოდი, მარგინალურად ასეც აღვიქვათ – შეკრების ოპერაციის ანალოგი სიმრავლეებში). ამ დროს, მიღებული სიმრავლის ზომის გასაგებად, გასაერთიანებელი სიმრავლეების კარდინალობები იკრიბება. მაგალითად, რატომღაც, თუ გვინდა ქართული ანბანის ასოებისა და ფიფქიას ზღაპრის ჯუჯების სიმრავლეების გაერთიანება, მიღებული სიმრავლის ზომა, ანუ კარდინალური რიცხვი იქნება 33 + 7 = 40.

საინტერესო ისაა, რომ ასეთი არითმეტიკული ოპერაციები კარდინალურ რიცხვებზე შესაძლებელია ჩავატაროთ უსასრულო სიმრავლეებისთვისაც. ვთქვათ, ნატურალურ რიცხვთა ℕ უსასრულო სიმრავლესა და რაღაც ერთელემენტიან სიმრავლეს ვაერთიანებთ (კიდევ ერთხელ, შეკრების ოპერაციის ანალოგი სიმრავლეებში). ინტუიციურად, შეიძლება ჩაითვალოს, რომ ნატურალურ რიცხვთა ℕ უსასრულო სიმრავლის ზომა ℵ0 ერთი ელემენტით გაიზრდება და უფრო დიდ სიმრავლეს მივიღებთ. ასე არ არის. სინამდვილეში, მიღებული სიმრავლე იგივე უსასრულო სიმრავლე დარჩება, რაც იყო, ანუ:

ℵ0 + 1 = ℵ0.

მოცემული გამოსახულება შეძლება იდეურად გადაიწეროს სხვანაირადაც:

∞ + 1 = ∞

რაც იმას ნიშნავს, რომ უსასრულობას თუ ერთით გავზრდით, ისევ უსასრულობას მივიღებთ.

ამ უცნაური ტოლობის დასამტკიცებლად განთქმულ აზრით ექსპერიმენტს მოვიშველიებ, სახელად “გილბერტის სასტუმრო”. წარმოვიდგინოთ, არსებობს სასტუმრო, რომელსაც ოთახების უსასრულო რაოდენობა აქვს. ოთახები 1-დან გადანომრილია (გამოდის, ნატურალური რიცხვების სიმრავლეა).

ისე მოხდა, რომ ყველა ოთახში უკვე თითო სტუმარია შესახლებული. ასეთ პირობებში, სასტუმროს კიდევ ერთმა ადამიანმა მიაკითხა, ოთახი მოითხოვა და ერგო კიდევაც; როგორ?
სასტუმროს ადმინისტრაციამ ოთახი 1-ის სტუმარი ოთახ 2-ში გადაიყვანა, ოთახი 2-ის სტუმარი — ოთახ 3-ში, ოთახი 3-ის სტუმარი — ოთახ 4-ში და ა.შ.. ასე სტუმრისთვის ოთახი 1 გათავისუფლდება.

ფაქტი, რომ უსასრულო რაოდენობის ოთახიანი სასტუმრო, რომელიც სავსე იყო, ერთ სტუმარს მაინც მასპინძლობს, ნიშნავს, რომ როცა თვლად უსასრულო სიმრავლეში კიდევ ერთ ელემენტს დაამატებ, ისევ იგივე თვლად უსასრულო სიმრავლეს მიიღებ, რაც კარდინალური რიცხვების ენაზე შემდეგნაირად ჩაიწერება: ℵ0 + 1 = ℵ0.

შეიძლება, მკითხველთაგან ზოგიერთისთვის მათემატიკური ჩანაწერი (ისე, როგორადაც აქამდე ვწერდით) უფრო ცხადია და ამოცანა ასეც განვიხილოთ. წარმოვიდგინოთ, ნატურალურ რიცხვთა ℕ {1,2,3,4,5,…} სიმრავლესა (სასტუმროს ოთახები პირვანდელი სტუმრებით) და ერთელემენტიან {a} სიმრავლეს (ახალი სტუმარი) ვაერთიანებთ. შედეგად მივიღებთ რაღაც P { a,1,2,3,4,5,…} სიმრავლეს (სასტუმროს ოთახები განახლებული სტუმრებით). თუ ვაჩვენებთ, რომ ℕ {1,2,3,4,5,…} – სა და P { a,1,2,3,4,5,…} – ს შორის ურთიერთცალსახა შესაბამისობაა, მაშინ მათი ზომები (კარდინალები) ტოლი ყოფილა და ჩვენი გამოსახულებაც სამართლიანია;

\begin{matrix}
\textit{P}: & a & 1 & 2 & 3 & 4 & \mathbf{5} & \cdots\\
& \Updownarrow & \Updownarrow & \Updownarrow & \Updownarrow & \Updownarrow &
\Updownarrow & \cdots \\
\textit{ℕ}: & 1 & 2 & 3 & 4 & 5 & 6 & \cdots
\end{matrix}

როგორც ვხედავთ, ახალი P სიმრავლის თითოეული ელემენტი ℕ სიმრავლის კონკრეტულ ელემენტს შეესაბამება და პირიქით (ოთახი 1 ახლა ოთახ 2-ს მიემართება, ოთახი 2 — ოთახ 3-ს და ა.შ. ხოლო a ახალი სტუმარი პირველ ოთახშია ). ურთიერთცალსახა შესაბამისობა არსებობს და შესაბამისად P და ℕ სიმრავლეები ტოლი ზომისაა, – ℕ სიმრავლის ელემენტებზე რაღაც ერთი ელემენტის დამატებამ მისი ზომა არ შეცვალა.

განვიხილოთ კიდევ ერთი საინტერესო არითმეტიკული ოპერაცია უსასრულობაზე. რას მივიღებთ, თუ ორ თვლად უსასრულო სიმრავლეს გავაერთიანებთ? აქაც, რომ დავფიქრდეთ ერთი სიმრავლის უსასრულოდ ბევრ ელემენტს მეორე სიმრავლის უსასრულოდ ბევრი ელემენტი ემატება და ჯამში, ინტუიციურად, თითქოს ორი უსასრულობის დამტევი, კიდევ უფრო დიდი სიმრავლე უნდა მივიღოთ, რაც წესით, ასე გამოისახება: ℵ0 + ℵ0 = 2ℵ0. თუმცა, სინამდვილეში, ეს არასწორია. ორი თვლადი უსასრულო სიმრავლე რომ გავაერთიანოთ, მაინც იგივე ზომის უსასრულო თვლად სიმრავლეს მივიღებთ. ანუ:

ℵ0 + ℵ0 = ℵ0

დასამტკიცებლად ისევ გილბერტის უსასრულო ოთახებიანი სასტუმრო განვიხილოთ, სადაც ისევ ყველა ოთახი (რომლებიც 1-დან გადანომრილია) დაკავებულია. რა მოხდება, თუკი ერთის მაგიერ უსასრულო რაოდენობის სტუმარი მიაკითხავთ და თითოეული მათგანი ოთახს მოითხოვს? სასტუმრო თითოეულს დააბინავებს.

ჭკვიანი ადმინისტრაცია ასე მოიქცევა,— ყოველი n ოთახის ბინადარს 2n ოთახში გადაიყვანს, ანუ ოთახი 1-ის ბინადარი ოთახ 2-ში გადავა, ოთახი 2-ის ბინადარი ოთახ 4-ში გადავა, ოთახი 3-ის ბინადარი ოთახ 6-ში და ა.შ.. გამოვა, რომ პირვანდელი ბინადრებიდან თითოეული ახლა ლუწი ნუმერაციის ოთახშია, ხოლო აბსოლუტურად ყველა კენტი ნუმერაციის ოთახი თავისუფალია, სადაც ახალი უსასრულო რაოდენობის სტუმრები შესახლდებიან.

სიმრავლეთა თეორია ჩვენი მსჯელობისთვის არსებითია და სტატიის თეზისის მტკიცების ტვირთის უძვირფასეს ნაწილს ატარებს. ფაქტი, რომ უსასრულობები არათუ კონკრეტულად მოცემული, არამედ გაზომვადი, ერთმანეთისგან განსხვავებული, ურთიერთდადარებადი და მეტიც, არითმეტიკულად მანიპულირებადია, ყვირილით ამტკიცებს ამ ცნების კონკრეტულ სამყაროში ცხად არსებობას. მათემატიკური აზროვნების უმყარესად მოცემულ სისტემურობას რომ გავეშვათ, ყველაფერი, რაც ახლა აღვწერეთ, ნახევარი საუკუნეა კომპიუტერულ მეცნიერებებს ესაფუძვლება და თავის დროზე, მეტაფიზიკის წელკავისგან თავჩაქინდრული მისტიკოსები ყველაზე ველურ ფანტაზიებში რომ ვერ დაუშვებდნენ, ისეთ მიკროსამყაროებს ქმნის. უსასრულობა რომ თავად რიცხვებივით ცხადი მათემატიკური სტრუქტურა არ იყოს, მატერიალური სამყაროს აღმწერი და შემფასებელი, სახლებში შუქი არ გვექნებოდა.

ბოლოთქმა

წინათქმაში დაპირებისამებრ, იმის მიუხედავად, რომ თხრობა, საკითხის მტკიცება მათემატიკურ მიმართულებებს ესაფუძვლებოდა, შევეცადე საყოველთაო ენით, დაწვრილმანებულად, საჭირო თეორიული ცოდნის წინსწრებით ახსნით, უსასრულობის ხელმისაწვდომი ბუნება ნათლად ჩამომეყალიბებინა მკითხველის აკადემიური სპეციალობის განურჩევლად. ჩემს ჩანაფიქრში არსებითი დისციპლინური კვეთის სრულფასოვნად წარმოჩენა იყო,- ჰუმანიტარ მკითხველს, წესით და რიგით, ნაკლები კავშირის მქონეს რთულ მათემატიკასთან, ის მნიშვნელოვანი საკითხები მსურდა გაეგო, რომლებიც უსასრულობის, როგორც საყოველთაოდ მრავალმხრივი ცნების, იმგვარ გააზრებაში დაეხმარებოდა, ღრმა ტექნიკურ ცოდნას რომ მოაქვს. იგივეგვარად, მინდოდა ტექნიკოსი მკითხველისთვის მისსავე საქმეში ხშირად შეხვედრადი მონაცემები იმ შინაარსმწვდომი მსჯელობით წარმომეჩინა, ჰუმანიტარულ მეცნიერებებს რომ ახასიათებთ. დისციპლინური კვეთა მნიშვნელოვანია, რადგან თუკი საზიარო საკითხისადმი ცოდნა დარგობრივად დისკრეტული იქნება, განვითარების გზაზე კოჭლობით სიარული მოგვიწევს.

მაშასადამე, კომპლექსური ცვლადის, ზღვრისა და სიმრავლეთა თეორიებით ბევრ კლასიკურ საკითხს ვუპასუხეთ, უსასრულობას აბსტრაქტულად, ბუნდოვნად, ხელშეუხებლად რომ წარმოაჩენდა. შემოუსაზღვრავი სიდიდის, როგორც მათემატიკური აზრის აბსტრაქციის სისტემის მრავალმხრივი აღწერით, წარმოვაჩინეთ რამდენად გასაგები, ნაცნობი და ხელმისაწვდომია იგი. არაერთგან ვახსენეთ ისიც, უსასრულობის ცნება რამდენად მნიშვნელოვან, საყოველთაო მოცემულობებს ესაფუძვლება, რამხელაა მისი, როგორც ანალიზური ხელსაწყოს როლი თანამედროვე ადამიანის მიღწევებსა და თუნდაც, ყოფაცხოვრებაში.

იმ მკითხველს, რომელიც ამ სტატიას რიგი მეტაფიზიკური ან თეოლოგიური საზრისების აბუჩად ჩაგდებაში ჩამითვლის, მინდა ვუთხრა, ჩემთვის ყველაფერი, რაც მეცნიერებას ესაფუძვლება, პატივსაცემია, მაგრამ სრულმნიშვნელოვანია ჭეშმარიტების ძიების გზა გავაგრძელოთ, აუხსნელი გარემოების შვებიანი მისტიციზმით არ მოვიხიბლოთ ისე, თაობებს ბრიყვული წარმოდგენებით დაწამვლისთვის რომ წირავს.

მოკლედ, როგორც ბაზ ლაითიერმა თქვა სათამაშოების ისტორიაში, – “უსასრულობისკენ… და იმის იქით!”.

ბიბლიოგრაფია

Churchill, Ruel V., and James Ward Brown. Complex Variables and Applications. 9th ed. New York: McGraw-Hill Education, 2013.

Adams, Robert A., and Christopher Essex. Calculus: A Complete Course. 9th ed. Don Mills, ON: Pearson Canada, 2017.

Aristotle. Physics. Translated by Robin Waterfield. Oxford: Oxford University Press, 1996.

Cunningham, Daniel W. Set Theory: A First Course. Cambridge: Cambridge University Press, 2016.

Cheng, Eugenia. Beyond Infinity: An Expedition to the Outer Limits of Mathematics. New York: Basic Books, 2017.

Long, A. A., ed. The Cambridge Companion to Early Greek Philosophy. Cambridge: Cambridge University Press, 1999.
Gamow, George. One Two Three… Infinity: Facts and Speculations of Science. New York: Viking Press, 1947.
Rucker, Rudy. Infinity and the Mind: The Science and Philosophy of the Infinite. New York: Bantam Books, 1982.
Wheelwright, Philip, ed. The Presocratics. New York: Odyssey Press, 1959.

^[1] Ruel V. Churchill and James Ward Brown, Complex Variables and Applications, 9th ed. (New York: McGraw-Hill Education, 2013), 50, fig. 25.

^[2] Robert A. Adams and Christopher Essex, Calculus: A Complete Course, 9th ed., Figure 1.2, 62, Chapter 1, “Limits and Continuity” (New York: Pearson, 2018).

^[3] Aristotle, Physics, trans. Robin Waterfield (Oxford: Oxford University Press, 1996), Book VI, Chapter 9.

^[4] ნატურალური რიცხვები ეწოდება მთელ დადებით რიცხვებს, მაგალითად 1,2,3,4,5… და ა.შ.. ნატურალური რიცხვები აღინიშნება ℕ – ით.

^[5] Bijection

^[6] Daniel W. Cunningham, Set Theory: A First Course (Cambridge: Cambridge University Press, 2016), 110.

^[7] Daniel W. Cunningham, Set Theory: A First Course (Cambridge: Cambridge University Press, 2016), 110.

^[8] რაციონალური რიცხვები ეწოდება რიცხვებს, რომელიც შეიძლება გამოისახოს როგორც ორი მთელი რიცხვის განაყოფი, მაგალითად c = a/b მაშინ, როცა b ≠ 0.

^[9] ნამდვილი რიცხვები ეწოდება ნებისმიერ დადებით, ნებისმიერ უარყოფით რიცხვსა და ნულს.

^[10] სტატიის საყოველთაოობის პირობიდან გამომდინარე, დაწვრილებით არ ვაყალიბებ კანტორის დიაგონალური არგუმენტის მტკიცებას, რთული მათემატიკური ანალიზის საჭიროების გამო. დაინტერესებულ მკითხველს შეუძლია იხილოს: For a concise overview of Cantor’s diagonal argument and its implications, see Eugenia Cheng, *Beyond Infinity: An Expedition to the Outer Limits of Mathematics* (New York: Basic Books, 2017).