კორექტორი: მარიამ გორდაძე
მდევარი, თბილისი, 2023
წინათქმა
JPEG (Joint Photographic Experts Group) გამოსახულების კუმშვის მკარგავი (lossy) ბუნების[1] ალგორითმია, რომელიც ციფრული სურათების ზომის ისე შესამცირებლად შეიქმნა, რომ ხარისხი მნიშვნელოვნად არ დაიკარგოს. ალგორითმის მკარგავი ბუნება მოიაზრებს მოცემულობას, რომ ფაილის ინფორმაციის ნაწილი კუმშვისას იკარგება. JPEG ადრიან ოთხმოცდაათიან წლებში შეიქმნა და დღესდღეობით ინტერნეტში ყველაზე ხშირად გამოყენებადი გამოსახულების შეკუმშვის ფორმატია.
JPEG -ის ალგორითმის გამორჩეული მახასიათებელი კუმშვის დონის ცვლილების შესაძლებლობაა, – მომხმარებელს შეუძლია, თავად აარჩიოს, რა დონით შეკუმშავს გამოსახულების ფაილს, ანუ გადაწყვიტოს, რა მასშტაბის ხარისხის დანაკარგი აწყობს ფაილის ზომაში მოგებისათვის. JPEG ალგორითმი ფართოდ გამოიყენება წრფივი ელფერის[2] (continues-tone) გრაფიკული გამოსახულებების მიმოქცევისას ციფრულ სივრცეებში. შესაბამისად, მოცემულ ალგორითმს ვხვდებით მრავალ სოფთვეარში, – ვებ-ბრაუზერებში, ფოტო დამუშავების პროგრამებსა და ციფრულ კამერებში.
მოცემულ ნაშრომში დაწვრილებით განვიხილავთ JPEG შეკუმშვის ალგორითმის რაობასა და მუშაობის წესს. ასევე წარმოვადგენთ MATLAB – ში დანერგილ ალგორითმის კოდსა და ამ კოდის ანალიზს.
ალგორითმის მოკლე მიმოხილვა
ძალიან ზოგადად, ალგორითმი გამოსახულებას მცირე ზომის ბლოკებად, – მიკრობლოკებად, – ყოფს და თითოეულ მათგანს უკეთებს დისკრეტულ კოსინუს გარდაქმნას (DCT). DCT თითოეული პიქსელის ინფორმაციას გარდაქმნის სიხშირულ კოეფიციენტებად, რის შედეგადაც შესაძლებელი ხდება გამოსახულების წარმოდგენა სიხშირულ სივრცეში. ამის შემდეგ ალგორითმი იწყებს კვანტიზაციას, – ამცირებს ამ კოეფიციენტების სიზუსტეს და აშორებს იმ მაღალსიხშირულ ინფორმაციას, რომელიც ისედაც არ არის ადამიანის თვალისათვის აღქმადი. ინფორმაციის მოშორების შემდეგ ვიღებთ უფრო პატარა ზომის ფაილს. საბოლოოდ კვანტიზებული კოეფიციენტები გაიშიფრება ენტროპიული კოდირებით.
ფერსივრცეები და მათი ცვლილება JPEG შეკუმშვის ალგორითმში
ფერსივრცე არის სისტემა, რომელიც ისე წარმოადგენს ფერებს, როგორადაც მათ ამუშავებს სხვადასხვა ხელსაწყო, – კომპიუტერი, ეკრანი, პრინტერი და ა.შ.. განსხვავებულ ფერსივრცეებს განსხვავებული ფერთა გამა აქვს, ანუ თითოეული მათგანი დამოუკიდებელი რაოდენობის ფერთა რიგს მოიცავს. ჩვენი საჭიროებებიდან გამომდინარე, განვიხილავთ ორ ფერსივრცეს: RGB-სა და YCBCR – ს.
RGB:
RGB (Red, Green, Blue) კრებადი ფერსივრცეა, რაც იმას ნიშნავს, რომ მის გამაში შემავალი ფერები მიიღება წითელი, მწვანე და ლურჯი სინათლეების სხვადასხვა პროპორციულობის შეკრებით. შესაბამისად, RGB – ს გამაში თითოეული ფერი წარმოდგენილია წითელი, მწვანე და ლურჯი ფერების გაერთიანებით.
სამიდან თითოეულ ფერს აქვს შესაბამისი მნიშვნელობა, რომელიც იცვლება 0 – დან 255 – ის ჩათვლით, – 0 არის ფერის არარსებობა, ხოლო 255 – ფერის მაქსიმალური ინტენსივობა, ანუ წმინდა წითელი ფერი წარმოდგება, როგორც (255,0,0); წმინდა მწვანე – (0,255,0); წმინდა ლურჯი – (0,0,255). ამ სისტემით მრავალი ფერის გამოსახვაა შესაძლებელი, მაგალითად: თეთრი, როგორც სამივე ფერის მაქსიმალური ინტენსივობა – (255,255,255); შავი, როგორც არცერთი ფერის არსებობა – (0,0,0); ნაცრისფერი, როგორც სამივე ფერის თანაბარი ინტენსივობა – (128,128,128).
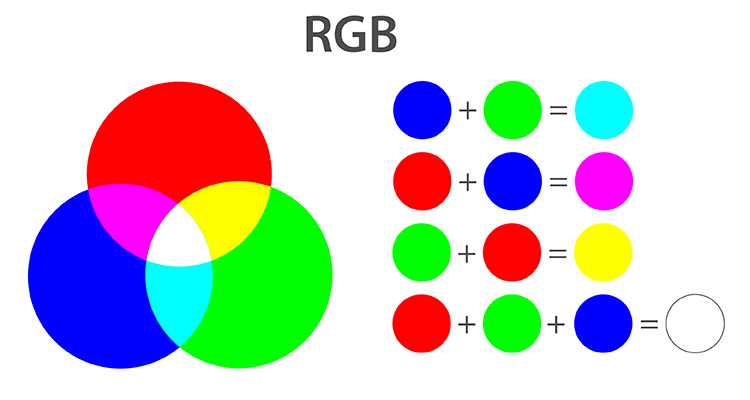
RGB ტექნოლოგიებში ყველაზე ხშირად გამოყენებადი ფერსივრცეა, რადგან შესაძლებლობას იძლევა, უმარტივესი წესით გამოისახოს უამრავი ფერი.
Y’CbCr:
Y’CbCr მკარგავი ბუნების არაკრებადი ფერსივრცეა, რომელიც აცალკევებს კაშკაშა ინფორმაციას (Y’) ქრომატული ინფორმაციისაგან (Cb & Cr). მსგავსი განცალკევება ფოტო და ვიდეო ინფორმაციის უფრო ეფექტური გაშიფვრისა და გადაცემის შესაძლებლობას ქმნის.
Y’CbCr ფერსივრცეში გამოსახულების თითოეული პიქსელი წარმოდგება სამი შემადგენელი ნაწილისაგან: Y’, Cb და Cr. Y’ ნაწილი წარმოადგენს პიქსელის სიკაშკაშეს, ხოლო Cb და Cr ნაწილები – პიქსელის ფერს; წარმოსადგენად, ესაა გამოსახულების განცალკევება შავ-თეთრ (ბნელი და ნათელი არეები), ლურჯ და წითელ ნაწილებად. Y’ კომპონენტი გამოყენება 8-ბიტიანი, ხოლო Cb და Cr ნაწილები 7-ბიტიანი სიზუსტით.

Y’CbCr ფერსივრცე განისაზღვრება ფერთა მატრიცითა და იმ კოეფიციენტების სიმრავლით, რომლებიც საჭიროა RGB – დან Y’CbCr – ში გამოსახულების გარდასაქმნელად.
უპირველესად, რასაც JPEG შეკუმშვისას ვიწყებთ, არის ფერსივრცის ცვლილება. საწყის (input) გამოსახულებას RGB – დან გარდავქმნით Y’CbCr ფერსივრცეში. ამის შემდეგ უკვე უფრო მარტივადაა შესაძლებელი გამოსახულების ფერებზე მუშაობა. არსებითი ისაა, რომ ადამიანის თვალი ძირითადად აღიქვამს გამოსახულების შავ-თეთრ (ბნელ და ნათელ) ნაწილს და ფერების განსაზღვრულ ინტენსივობას. ანუ, შეგვიძლია გამოსახულებაში ფერთა ინტენსივობა შევცვალოთ ისე, რომ ამ გამოსახულების ცვლილება არ იყოს ადამიანის ხედვის აპარატისთვის არსებითი, არ გვქონდეს მნიშვნელოვანი ხარისხობრივი დანაკარგი, რაც შესაძლებლობას გვაძლევს დავზოგოთ ფაილის ზომის ხარჯები. ზუსტად ამისთვის ისეთი ფერსივრცის გამოყენება (ჩვენს შემთხვევაში Y’CbCr), რომელიც თავისთავად წარმოადგენს გამოსახულების კაშკაშა და ქრომატულ ნაწილებს ცალ-ცალკე, ცალსახად ლოგიკურია.
MATLAB:
% კოდი 1: შემავალი სურათის ფერსივრცის ცვლილება
A = imread ('bird.png');
ycbcr = rgb2ycbcr(A);
temp = ycbcr;
Y = ycbcr(:,:,1); % Y channel
cb = ycbcr(:,:,2); % cb channel
cr = ycbcr(:,:,3); % cr channel
დისკრეტული კოსინუს გარდაქმნა (DCT)
ფერსივრცის შეცვლის შემდეგ ვიწყებთ DCT გარდაქმნას, მაგრამ ამის განხილვამდე მოკლედ მიმოვიხილოთ ამ ტექნიკის შინაარსი.
დისკრეტული კოსინუს გარდაქმნა მკარგავი ბუნების მათემატიკური ტექნიკაა, რომელიც ხშირად გამოიყენება ფოტო და ვიდეო დამუშავებაში იმისათვის, რომ ინფორმაცია წარმოდგეს სიხშირულ სივრცეში. DCT ფურიე გარდაქმნის ერთ-ერთი სახეა, ანუ იგი სიგნალს ყოფს სხვადასხვა სიხშირის მქონე პერიოდული ფუნქციების (ამ შემთხვევაში კოსინუსების) ჯამად. DCT- ის დანერგვა ყველაზე ხშირია სწრაფი ფურიე გარდაქმნით (FFT) და მეორე რიგის DCT – ით (type-II DCT). შემავალი სიგნალი (ჩვენს შემთხვევაში სურათი) იყოფა ბლოკებად (ჩვენს შემთხვევაში პიქსელებად) და DCT გარდაქმნა ხორციელდება თითოეულ ბლოკზე ცალ-ცალკე. გამომავალი სიგნალი უკვე წარმოდგენილია სიხშირული კოეფიციენტების სიმრავლის სახით, რაც საბოლოოდ არის შემავალი სიგნალის წარმოდგენა სიხშირულ სივრცეში.
მრავალ ბუნებრივ გამოსახულებაში[4] ენერგიის (პიქსელების მნიშვნელობების კვადრატების ჯამი) ძირითადი ნაწილი თავმოყრილია მცირეოდენ დაბალსიხშირულ კომპონენტებში. გამოსახულების სიხშირულ სივრცეში წარმოდგენით შესაძლებელი ხდება მაღალი ენერგიის მქონე ელემენტების მოშორება ისე, რომ გამოსახულების ხარისხი მნიშვნელოვნად არ შეიცვალოს. ანუ, უკვე მრავალჯერ ახსნილი ლოგიკით, გამოსახულებას ვაშორებთ ისედაც არაღქმად მაღალსიხშირულ ელემენტებს, – პრაქტიკულად, სურათში „ვცვლით ფერების რაოდენობას“.
DCT – ის გამოსახულებაზე გამოსაყენებლად სურათი იყოფა 8×8 – ზე მატრიცის პიქსელების ბლოკებად, რის შემდეგაც თითოეულ ბლოკზე ცალ-ცალკე ვიყენებთ DCT გარდაქმნას, რაც შედეგად გვაძლევს სიხშირულ სივრცეზე დამოკიდებულ კოეფიციენტებს. ანუ ჩვენი მატრიცის თითოეული ელემენტი წარმოდგება საკუთარი კოსინუსოიდით.

MATLAB:
% კოდი 2: გამოსახულების ბლოკებად დაყოფა->თითოეული ბლოკის შეკუმშვა
% Divide image by 8x8 pixel blocks.
blocks = im2col(ycbcr(:,:,j), [8 8], 'distinct');
compressed_blocks = [];
% compress every block.
for i = 1:size(blocks, 2)
compressed_block = jpegcompress(blocks(:, i));
% Save compressed.
compressed_blocks(:,i) = compressed_block;
end
[5]DCT განტოლება განისაზღვრება, როგორც:
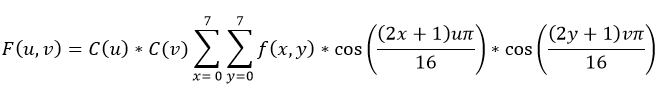
მოცემული განტოლება განსაზღვრავს სიხშირულ კოეფიციენტ F(u,v) – ს (u,v) ადგილას, გარდაქმნამდელ ბლოკში პიქსელების მნიშვნელობების, f(x,y) – ის მიხედვით. u და v ცვლადების მნიშვნელობები მოქცეულია 0 – დან 7-მდე რიგში და წარმოადგენენ სხვადასხვა სიხშირულ კომპონენტს ბლოკებში. მუდმივები, – C(u) და C(v), – განისაზღვრებიან შემდეგნაირად:
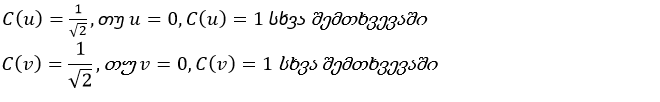
მიღებულ სიხშირულ სივრცეზე დამოკიდებულ კოეფიციენტებს ვუკეთებთ კვანტიზაციას კვანტიზაციის ცხრილის მიხედვით. კვანტიზაციის ცხრილით დგინდება ის გაფართოება (Resolution), რომელზედაც კოეფიციენტები არიან წარმოდგენილნი. კვანტიზაციისას თითოეული სიხშირული კოეფიციენტი იყოფა კვანტიზაციის ცხრილის შესაბამის მნიშვნელობაზე და მიღებული შედეგი მრგვალდება უახლოეს მთელ რიცხვამდე, მაღალსიხშირული კომპონენტებისთვის ეს მნიშვნელობა უმეტესად ნულის ტოლია.
კვანტიზაციას შეკუმშვაში არსებითი როლი აქვს, – იმ გაფართოების შემცირებით, რომელზედაც წარმოდგენილნი არიან შესაბამისი სიხშირული კოეფიციენტები, შესაძლებელი ხდება გამოსახულების ინფორმაციის ზომის მნიშვნელოვნად შემცირება. გასათვალისწინებელია, რომ სურათის ხარისხი შეიძლება მნიშვნელოვნად დაიკარგოს, თუკი კვანტიზაცია იქნება ძალიან მასშტაბური. სხვადასხვა ხარისხის კუმშვისთვის გამოიყენება სხვადასხვა კვანტიზაციის ცხრილი.
MATLAB:
% კოდი 3: შეკუმშვა, კვანტიზაცია
function compressed_block = jpegcompress(block)
% Transform the block using the
%discrete cosine transform (DCT)
block = double(block) - 128;
compressed_block = dct2(block);
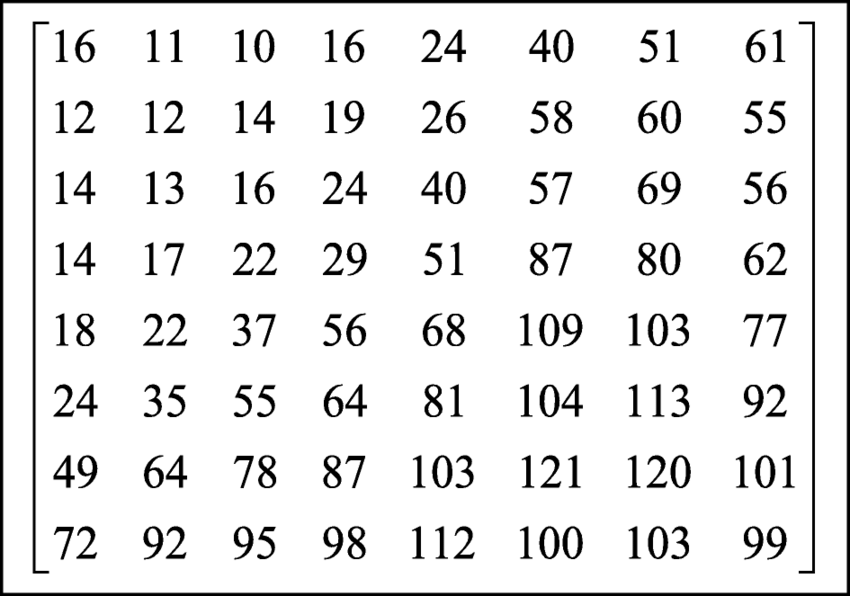
% Quantize Table
quant_table = round([16 11 10 16 24 40 51 61 12 12 14 19 26 58 60 55 14 13 16 24 40 57 69 56 14 17 22 29 51 87 80 62....
18 22 37 56 68 109 103 77 24 35 55 64 81 104 113 92 49 64 78 87 103 121 120 101 72 92 95 98 112 100 103 99]);
% Quantize DCT Coefficients
compressed_block = round (compressed_block ./ quant_table');
end
განკუმშვისას კვანტიზებური სიხშირული კოეფიციენტები უკუკვანტიზდება (ანუ მრავლდება კვანტიზაციის ცხრილის შესაბამის მნიშვნელობაზე. კვანტიზაციისას განულებული მაღალსიხშირული კომპონენტების კოეფიცინეტების ამგვარად აღდგენა შეუძლებელია, აქ გამოიხატება კუმშვის ფორმატის მკარგავი ბუნება). შემდეგ ვმოქმედებთ უკუ – დისკრეტული კოსინუს გარდაქმნით (IDCT) იმისათვის, რომ მივიღოთ პირვანდელი სურათის კონკრეტულ ბლოკებთან მიახლოებული ბლოკები. როცა აბსოლუტურად ყველა ბლოკი დამუშავდება, მიღებული ბლოკების ერთობა იქნება საბოლოო, განკუმშული გამოსახულება.
MATLAB:
% კოდი 4: განკუმშვა, უკუკვანტიზაცია
function decompressed_block = jpegdecompress(compressed_block)
% Quantize Table
quant_table = round([16 11 10 16 24 40 51 61 12 12 14 19 26 58 60 55 14 13 16 24 40 57 69 56 14 17 22 29 51 87 80 62....
18 22 37 56 68 109 103 77 24 35 55 64 81 104 113 92 49 64 78 87 103 121 120 101 72 92 95 98 112 100 103 99]);
% Unquantize compressed_block.
decompressed_block = compressed_block.*quant_table';
% Inverse DCT:
decompressed_block = idct2(decompressed_block);
% Don't forget to add 128.
decompressed_block = decompressed_block + 128;
end
JPEG ალგორითმის უშუალო ზემოქმედება განსხვავებული ფოტოების მაგალითზე
ბუნებრივია, JPEG შეკუმშვა სხვადასხვა ტიპის ფოტოზე განსხვავებული წარმატებით მოქმედებს (წარმატება განისაზღვრება სურათის ხარისხის ნაკლებად დაკარგვით). შეკუმშვის ალგორითმისა და მრავალჯერ ახსნილი ლოგიკიდან გამომდინარე, მაღალსიხშირული ინფორმაციის მატარებელი პიქსელების შემადგენლობის ფოტოები მეტად კარგავენ ხარისხს, ვიდრე – დაბალსიხშირულები. ხარისხის შესაფასებლად შესაძლებელია გამოვიყენოთ როგორც თვალი, რაც არ არის ობიექტური შემფასებელი, ასევე მათემატიკური მეთოდი- PNSR (Peak Signal-to-Noise Ratio). PSNR-ის მნიშვნელობა გვიჩვენებს, თუ რამდენად წარმატებული აღმოჩნდა სურათის შეკუმშვა: რაც მეტია მისი მნიშვნელობა, მით უკეთესია შეკუმშული სურათის ხარისხი. მიჩნეულია, PSNR > 30db, არის პირვანდელთან კარგი თანაფარდობის მქონე ხარისხის შეკუმშვა, ხოლო PSNR < 20db – ცუდი.
PSNR-ის გასაგებად, პირველ რიგში, საჭიროა დავთვალოთ საშუალო კვადრატული ცდომილება (Mean Squared Error) პირვანდელ და შეკუმშულ სურათებს შორის ფორმულით:
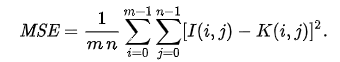
შემდეგ გამოვიყენოთ PSNR-ის დასათვლელ ფორმულაში:
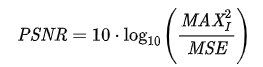
სადაც MAXi წარმოადგენს პიქსელის უმაღლესი სიკაშკაშის დონეს (RGB-ს შემთხვევაში 255-ს).
MATLAB:
% კოდი 5: PSNR
mse = sum((A(:) - AA(:)).^2) / numel(A);
psnr = 10 * log10(255^2 / mse)
აღწერილის თვალსაჩინოებისთვის განვიხილოთ რამდენიმე სურათი: bird.png, fox.png.
bird.png:
პირვანდელი

შეკუმშული

fox.png:
პირვანდელი

შეკუმშული

JPEG ალგორითმის დანერგვა MATLAB-ში, სრული კოდი:
myJPEG.m
A = imread ('bird.png');
ycbcr = rgb2ycbcr(A);
temp = ycbcr;
Y = ycbcr(:,:,1); % Y channel
cb = ycbcr(:,:,2); % cb channel
cr = ycbcr(:,:,3); % cr channel
% for every colorspace component:
for j = [1 2 3]
% Divide image by 8x8 pixel blocks.
blocks = im2col(ycbcr(:,:,j), [8 8], 'distinct');
compressed_blocks = [];
% compress every block.
for i = 1:size(blocks, 2)
compressed_block = jpegcompress(blocks(:, i));
% Save compressed.
compressed_blocks(:,i) = compressed_block;
end
decompressed_blocks = [];
% decompress blocks.
for i = 1:size(compressed_blocks, 2)
compressed_block = compressed_blocks(:,i);
% Decompress block.
decompressed_block = jpegdecompress(compressed_block);
decompressed_blocks(:,i) = decompressed_block;
end
% Recreate Y component of the image.
jpg = col2im(decompressed_blocks, [8 8], size(A), 'distinct');
% show uncompressed image.
ycbcr(:,:,j) = jpg;
end
AA = ycbcr2rgb(ycbcr);
subplot(1,2,1);
imshow (uint8(AA));
title ('Compressed');
subplot(1,2,2);
imshow(A);
title ('Original');
% Measure compression quality.
% psnr > 30 db is generally considered as good compression quality.
% psnr < 20 db is considered as bad.
mse = sum((A(:) - AA(:)).^2) / numel(A);
psnr = 10 * log10(255^2 / mse)
jpegcompress.m
function compressed_block = jpegcompress(block)
% Transform the block using the
%discrete cosine transform (DCT)
block = double(block) - 128;
compressed_block = dct2(block);
% Quantize Table
quant_table = round([16 11 10 16 24 40 51 61 12 12 14 19 26 58 60 55 14 13 16 24 40 57 69 56 14 17 22 29 51 87 80 62....
18 22 37 56 68 109 103 77 24 35 55 64 81 104 113 92 49 64 78 87 103 121 120 101 72 92 95 98 112 100 103 99]);
% Quantize DCT Coefficients
compressed_block = round (compressed_block ./ quant_table');
end
jpegdecompress.m
function decompressed_block = jpegdecompress(compressed_block)
% Quantize Table
quant_table = round([16 11 10 16 24 40 51 61 12 12 14 19 26 58 60 55 14 13 16 24 40 57 69 56 14 17 22 29 51 87 80 62....
18 22 37 56 68 109 103 77 24 35 55 64 81 104 113 92 49 64 78 87 103 121 120 101 72 92 95 98 112 100 103 99]);
% Unquantize compressed_block.
decompressed_block = compressed_block.*quant_table';
% Inverse DCT:
decompressed_block = idct2(decompressed_block);
% Don't forget to add 128.
decompressed_block = decompressed_block + 128;
end
ბოლოთქმა
მოცემულ სტატიაში საფუძვლიანად განვიხილეთ JPEG კუმშვის ალგორითმის სტრუქტურა, მისი თითოეული კონსტრუქტი, ალგორითმთან დაკავშირებული ყველა საჭირო ცნება და საბოლოოდ მისი დანერგილი კოდი MATLAB – ში.
JPEG კუმშვის ალგორითმი ძალიან ჭკვიანური, ეფექტური შესაძლებლობაა ფაილთა ზომების ოპტიმიზაციისათვის. დანერგვის თვალსაზრისით, საკმაოდ კომპლექსური კომპოზიციაა, თუმცა MATLAB-ში ჩაშენებული მეთოდები მოქმედებას ამარტივებს.
შევეცადეთ, ალგორითმი დაგვენერგა ყველაზე უფრო ცხადი ტექნიკებით, თუმცა ალგორითმის დასანერგად აღსანიშნავად საინტერესო გზაა უდანაკარგო ბუნების გაშიფვრის ალგორითმის, – “Huffman-ის“, – გამოყენებაც.
ბიბლიოგრაფია:
- stevewhims. “JPEG YCbCr Support – Win32 Apps.” JPEG YCbCr Support – Win32 apps | Microsoft Learn, January 7, 2021. https://learn.microsoft.com/en-us/windows/win32/wic/jpeg-ycbcr-support.
- Gonzalez, Rafael C., Richard Eugene Woods, and Steven L. Eddins. Digital image processing using MATLAB. Pearson Education India, 2004. http://sdeuoc.ac.in/sites/default/files/sde_videos/Digital%20Image%20Processing%203rd%20ed.%20-%20R.%20Gonzalez%2C%20R.%20Woods-ilovepdf-compressed.pdf
- Khayam, Syed Ali. “The discrete cosine transform (DCT): theory and application.” Michigan State University 114, no. 1 (2003): 31. http://rmarsh.cs.und.edu/CLASS/CS446/DiscreteCosineTransform.pdf
[1] მკარგავი ბუნების სისტემები, ოპერაციები და ა.შ. ისეთი მოქმდებებია, რომელთა შედეგადაც გვაქვს გარკვეული ხარისხის დანაკარგი.
[2] წრფივი ელფერის გამოსახულებები ისეთი სურათებია, რომელთაც გააჩნიათ ფერებისა და ელფერების წრფივი რიგი, – შავიდან თეთრამდე (ყველაზე ბნელი ფერიდან ყველაზე ნათელ ფერამდე). ასეთი სურათები უფრო რეალისტურია დიდი ფერთა გამის არსებობის გამო. წრფივი ელფერის გამოსახულებების საპირისპიროა დისკრეტული ელფერის გამოსახულებები, ანუ სურათები, რომელთაც მხოლოდ განსაზღვრული რაოდენობის ფერები და ელფერები აქვთ.
[3] stevewhims. “JPEG YCbCr Support – Win32 Apps.” JPEG YCbCr Support – Win32 apps | Microsoft Learn, January 7, 2021. https://learn.microsoft.com/en-us/windows/win32/wic/jpeg-ycbcr-support.
[4] გამოსახულებების შეკუმშვის ჭრილში „ბუნებრივი გამოსახულებები“ ზოგადად მოიაზრებს სურათებს, რომლებიც გამოსახავენ ნამდვილი გარესამყაროს პერიფერიებს, საგნებს. „ბუნებრივი გამოსახულებები“ შეიძლება იყოს ფოტო, ვიდეო ან ნებისმიერი სხვა სახის გამოსახულება, რომელიც გადაღებულია კამერით ან სხვა ოპტიკური ხელსაწყოთი.
[5] 1. Khayam, Syed Ali. “The discrete cosine transform (DCT): theory and application.” Michigan State University 114, no. 1 (2003): 31.
